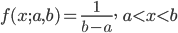
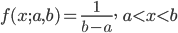
![{\rm E}[X] = \int^b_a \ \frac{x}{b-a} dx= \Bigl[ \frac{x^2}{2(b-a)} \Bigr]^b_a = \frac{b^2-a^2}{2(b-a)}=\frac{a+b}{2}](images/EXTERN_0001.png)
![{\rm Var}[X]={\rm E}[X^2]-({\rm E}[X])^2 = \int^b_a \ \frac{x^2}{b-a}dx- \frac{(a+b)^2}{4}=\frac{b^3-a^3}{3(b-a)}-\frac{(a+b)^2}{4}](images/EXTERN_0002.png)

| x <- runif(10000) | #(0,1)一様乱数1000個列 |
| hist(x, main="(0, 1) 一様乱数 10000個") | #ヒストグラム表示 |
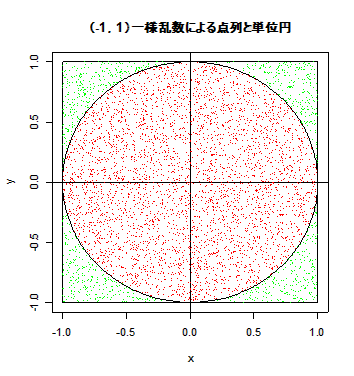
| n <- 10000 | #一様乱数の個数 |
| x <- runif(n, -1, 1) | #(-1, 1) の範囲の一様乱数 n 個生成 |
| y <- runif(n, -1, 1) | # |
| r <- x^2 + y^2 | #原点からの距離の2乗 |
| plot(x,y, type="n", xlim=c(-1,1), ylim=c(-1,1)) | #グラフの表示範囲の指定 |
| abline(h=0) | # x 軸の表示 |
| abline(v=0) | # y 軸の表示 |
| segments(-1, 1, 1, 1) | #(-1, 1)から(1, 1)までの直線 |
| segments(1, 1, 1, -1) | # |
| segments(-1, -1, 1, -1) | # |
| segments(-1, -1, -1, 1) | # |
| pin <- (1:n)[r<1] | #乱数のうち単位円内に入る乱数の番号 |
| points(x[-pin], y[-pin], pch=".", col="green") | #単位円の外の乱数を緑点で表示 |
| points(x[pin], y[pin], pch=".", col="red") | #単位円内の乱数を赤い点で表示 |
| s <- 0:360 | # 0 度から 360 度 |
| theta <- s*pi/180 | #度をラジアンに変換 |
| xp = sin(theta) | #単位円の x 座標 |
| yp = cos(theta) | #単位円の y 座標 |
| points(xp,yp, type="l") | #単位円を表示 |
| title(main="(-1,1)一様乱数による点列と単位円") | |
| length(pin) | #単位円内に入った乱数の個数 |
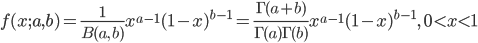
![{\rm E}[X^r] = \frac{1}{B(a, \ b)} \int^1_0 x^{r+a-1}(1-x)^{b-1} dx = \frac{B(r+a, \ b)}{B(a, \ b)}](images/EXTERN_0006.png)
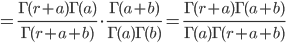
![{\rm E}[X] = \frac{\Gamma(a+1)\Gamma(a+b)}{\Gamma(a)\Gamma(a+b+1)}=\frac{a! (a+b-1)!}{(a-1)! (a+b)!}=\frac{a}{a+b}](images/EXTERN_0008.png)
![{\rm Var}[X]={\rm E}[X^2]-({\rm E}[X])^2 = \frac{\Gamma(a+2)\Gamma(a+b)}{\Gamma(a)\Gamma(a+b+2)}- \Bigl(\frac{a}{a+b} \Bigr)^2](images/EXTERN_0009.png)
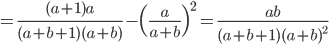
|
|
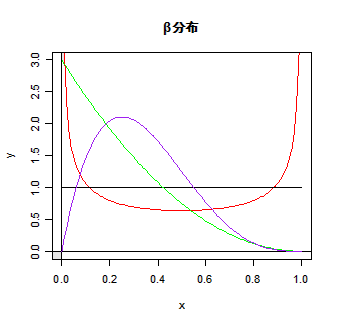
| x <- seq(0,1, by=0.01) | # x の定義 0 から 1 まで 0.01 きざみ |
| y <- dbeta(x, 0.5, 0.5) | # a, b = 0.5, 0.5 のβ分布 |
| plot(x, y, type="l", ylim=c(0,3), col="red") | # y を 0 から 3 に指定(赤) |
| abline(v=0, h=0) | # y 軸と x 軸の表示 |
| curve(dbeta(x, 1, 1), 0, 1, add=T) | # a, b = 1, 1 のβ分布 |
| curve(dbeta(x, 2, 2), 0, 1, add=T, col="blue") | # a, b = 2, 2 のβ分布(青) |
| curve(dbeta(x, 1, 3), 0, 1, add=T, col="green") | # a, b = 1, 3 のβ分布(緑) |
| curve(dbeta(x, 2, 4), 0, 1, add=T, col="purple") | # a, b = 2, 4 のβ分布(紫) |
| title(main="β分布") | # |
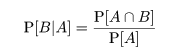 |
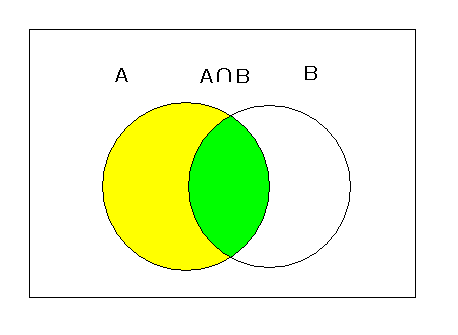 |
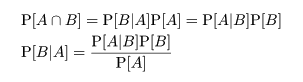
となり,約 9%で感染確率はそれほど高くない.これは,もともとの感染率(事前確率)が 0.1%と
低リスクなので,陽性反応が出たという情報を得たことで
感染確率(リスク)は約90倍上がるがまだ悲観するには
あたらない.
しかし,これは非感染でも検査薬が 1%は間違えるということがあるからである.もともとの
感染率 0.1%に比べ,検査薬の間違え率が10倍高いので,陽性反応が出たといっても間違えた可能性
の方が高いと判断できるからである.もし,技術進歩により非感染の場合99.9%陰性反応が出るように
なったとすると,
となり一気に跳ね上がる.これは,感染率と検査薬の間違え率が同じなので,感染と間違えが 5分 5分 であるからである.
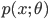 と記述される.しかし,パラメータ θ がある事前分布(prior distribution)
と記述される.しかし,パラメータ θ がある事前分布(prior distribution)
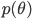 を持つと想定するときは,データ分布は事前分布のあるパラメータの値 θ での条件付き分布(conditional distribution)
を持つと想定するときは,データ分布は事前分布のあるパラメータの値 θ での条件付き分布(conditional distribution)
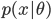 の形で記述される.このとき,x と θ の同時分布(joint distribution)は,
の形で記述される.このとき,x と θ の同時分布(joint distribution)は,
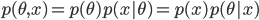
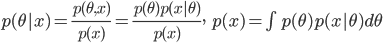
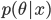 を θ の事後分布(posterior distribution)という.x の周辺分布(marginal distribution)である分母の
を θ の事後分布(posterior distribution)という.x の周辺分布(marginal distribution)である分母の
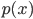 の計算が面倒なときは,分母を無視して,
の計算が面倒なときは,分母を無視して,
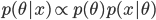
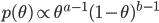
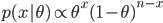
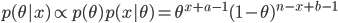
![{\rm E}[\theta |x]=\frac{x+a}{n+a+b}](images2/EXTERN_0011.png)
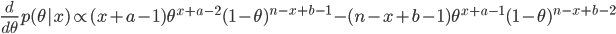
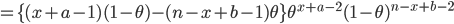
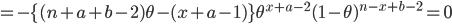
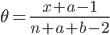
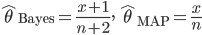
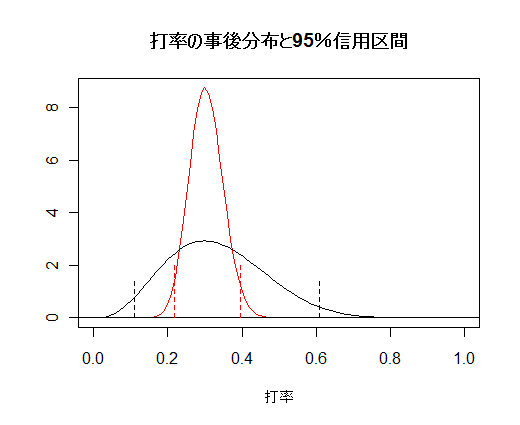
n1 <- 10; x1 <- 3 c1 <- qbeta(c(0.025, 0.975), x1+1, n1-x1+1); c1 # 事後ベータ分布の95%区間 n2 <- 100; x2 <- 30 c2 <- qbeta(c(0.025, 0.975), x2+1, n2-x2+1); c2 curve(dbeta(x, x2+1, n2-x2+1), 0, 1, col="red", xlab="打率", ylab="") curve(dbeta(x, x1+1, n1-x1+1), 0, 1, add=T) abline(h=0) segments(c2[1], 0, c2[1], 2, lty=2, col="red") segments(c2[2], 0, c2[2], 2, lty=2, col="red") segments(c1[1], 0, c1[1], 1.5, lty=2) segments(c1[2], 0, c1[2], 1.5, lty=2) title(main="打率の事後分布と95%信用区間") |

n1 <- 300; x1 <- 90 # 昨年の成績 x <- seq(0.1, 0.5, by=0.001) plot(x, dbeta(x, x1+1, n1-x1+1), type="l", ylim=c(0,17), xlab="打率", ylab="") # 事前分布の更新 abline(h=0) n2 <- 20; x2 <- 0 # 今年の成績 y <- dbeta(x, x2+x1+1, n2-x2+n1-x1+1) lines(x, y, col="red") # 今年の事後分布 p <- 0.25 # スランプとみなす打率 y2 <- dbeta(p, x2+x1+1, n2-x2+n1-x1+1) xx <- seq(0.1, p, by=0.001) yy <- dbeta(xx, x2+x1+1, n2-x2+n1-x1+1) segments(p, 0, p, y2, col="red") polygon(c(xx, p, 0.1), c(yy, 0, 0), col="red", density=8) title(main="事前分布の更新によるスランプ確率") pbeta(p, x2+x1+1, n2-x2+n1-x1+1) # スランプの確率 |
p <- 0.25 (1-p)^20 # 20 打席ノーヒット 20*p*(1-p)^19 # 20 打席 1 安打 |
となる.このとき,
とおくと,ベータ分布の平均と分散はそれぞれ,
となる.
ベータ二項分布は x と p の同時分布を p で積分して
周辺化した x の周辺分布(marginal distribution)である.すなわち,
となる.ベータ分布で θ → 0 とすると,Var[p] → 0 となり,ベータ分布は μ に集中 した分布に退化する.このとき,Var[x] → nμ(1-μ) になり,ベータ二項分布は二項分布 Binom(n, μ) に収束する.
| 女児数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 度数 | 7 | 45 | 181 | 478 | 829 | 1112 | 1343 |
| 女児数 | 7 | 8 | 9 | 10 | 11 | 12 | 合計 |
| 度数 | 1033 | 670 | 286 | 104 | 24 | 3 | 6115 |
このデータの平均,分散はそれぞれ,
となった.単純な二項分布モデルを考えると女児の生まれる確率の推定値 p^ は,
となる.データが二項分布に従っているなら,その平均,分散はそれぞれ,
となるはずである.しかし,データの分散 3.49 はこの想定される分散より大きい
ので,過分散になっていると考えられる.
そこで,ベータ二項分布にデータをあてはめることを考える.ここでは,単純なモーメント法
によるパラメータ推定を行ってみる.すなわち,データの平均と分散が想定分布の平均と分散
と等しいとおくのである.
の連立方程式を解くと,
となる.これより,女児の生まれる確率 p が従うベータ分布のパラメータは,
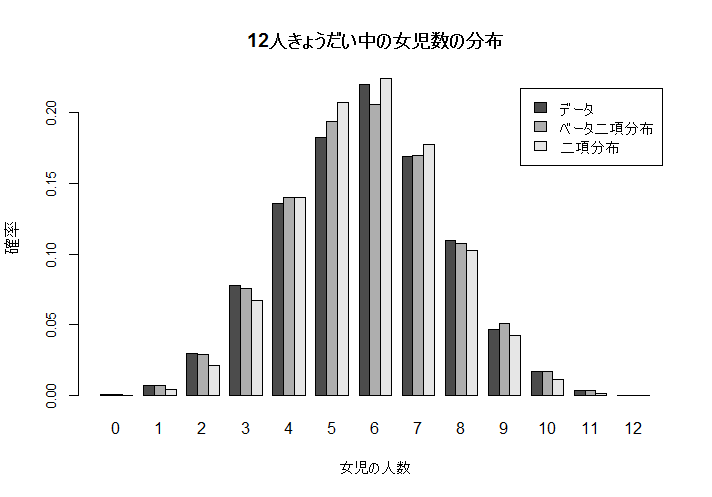
となり,家系による女児出生確率のばらつきが推定された.
n <- 12
x <- 0:n
girl <- c(7,45,181,478,829,1112,1343,1033,670,286,104,24,3)
sum(girl)
pgirl <- girl/sum(girl)
m <- sum(x*pgirl) # 平均
p <- m/n # 女児出生確率推定値
# これがベータ分布の平均μになる.
v <- sum(pgirl*(x-m)^2) # 分散
v1 <- n*p*(1-p)
h1 <- dbinom(x, n, p) #
# ベータ分布パラメータ
th <- (v - v1)/(n*v1 - v)
a <- p/th
b <- (1-p)/th
# ベータ二項分布の確率密度
y <- lchoose(n, x) + lbeta(x+a, n-x+b) - lbeta(a,b)
h2 <- exp(y)
mb <- sum(x*h2); mb
sum(h2*(x-mb)^2)
#
girldis <- rbind(pgirl, h2, h1)
colnames(girldis) <- as.character(0:n)
barplot(girldis, beside=TRUE, cex.axis=0.8, cex.lab=1.0, xlab="女児の人数", ylab="確率",
legend=c("データ","ベータ二項分布", "二項分布"))
title(main="12人きょうだい中の女児数の分布")
#
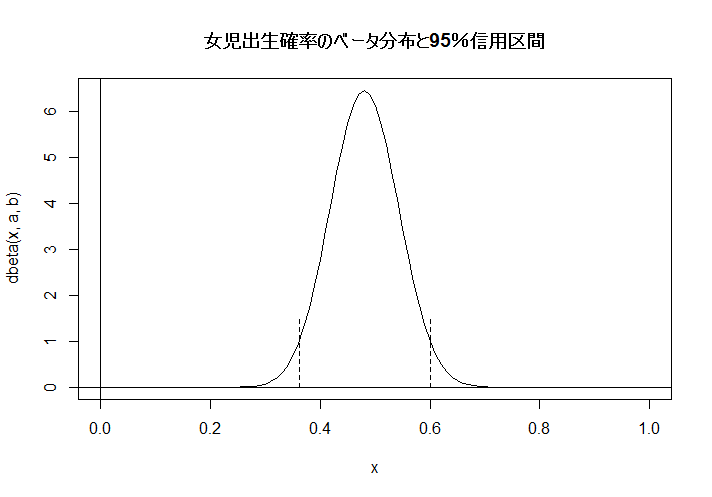
c1 <- qbeta(c(0.025, 0.975), a, b); c1
curve(dbeta(x, a, b), 0, 1)
abline(v=0, h=0)
title(main="女児出生確率のベータ分布と95%信用区間")
segments(c1[1], 0, c1[1], 1.5, lty=2)
segments(c1[2], 0, c1[2], 1.5, lty=2)
|
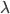 をもつ確率密度関数が
をもつ確率密度関数が
![m(t) = {\rm E}[e^{tX}] = \frac{\lambda}{\lambda-t}, \ t<\lambda](images/EXTERN_0013.png)
![{\rm E}[X] = \frac{1}{\lambda}](images/EXTERN_0014.png) , 分散:
, 分散: ![{\rm Var}[X] = \frac{1}{\lambda^2}](images/EXTERN_0015.png)
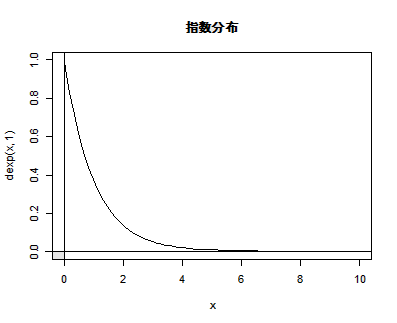
| curve(dexp(x, 1), 0, 10) | #指数分布の密度関数 |
| abline(v=0, h=0) | # y 軸,x 軸表示 |
| title(main="指数分布") | # |
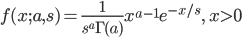
![m(t)={\rm E}[e^{tX}] = \int^\infty_0 \frac{1}{s^a \Gamma(a)} e^{tx} x^{a-1} e^{-x/s} dx](images/EXTERN_0017.png)
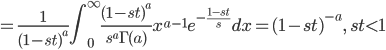
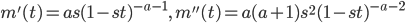
![{\rm E}[X] = m'(0)=as](images/EXTERN_0020.png)
![{\rm Var}[X]={\rm E}[X^2]-({\rm E}[X])^2 = m''(0)-(as)^2 = a(a+1)s^2-a^2s^2 = as^2](images/EXTERN_0021.png)
|
|
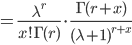
![\int^\infty_0 \frac{[(\lambda+1)\theta]^{r+x-1}e^{-(\lambda+1)\theta}}{\Gamma(r+x)} d[(\lambda+1)\theta]](images/EXTERN_0026.png)
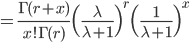
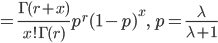
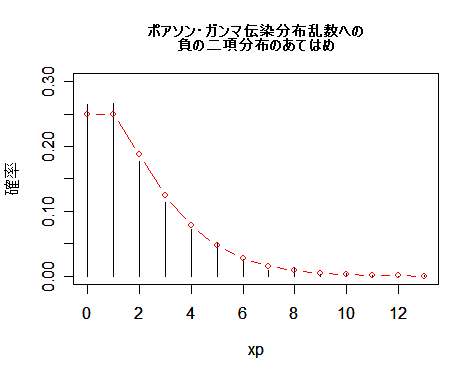
| n <- 1000 | # 伝染分布乱数の個数 |
| count <- NULL | # count の定義 |
| for(i in 1:n){ | # n 回の繰り返し |
| r <- 2 | # ガンマ分布のシェープパラメータ |
| lam <- 1 | # ガンマ分布のレイトパラメータ |
| theta <- rgamma(1, r, lam) | # ガンマ分布乱数1つ生成 |
| count <- c(count, rpois(1, theta)) | # 生成乱数をパラメータにするポアソン乱数列 |
| } | # |
| mc <- max(count) | # ポアソン・ガンマ乱数列の最大値 |
| xp <- 0:mc | # 個数の定義域 |
| d <- factor(count, levels=xp) | # 個数が 0 の階級も含める |
| table(d) | # メッシュ内個数の階級区分 |
| s <- sum(table(d)) | # 総個体数 |
| m1 <- sum(xp*table(d)/s) | # カウント分布の平均 |
| v1 <- sum(table(d)/s*(xp-m1)^2) | # カウント分布の分散 |
| plot(xp, table(d)/s, type="h", ylim=c(0,0.3), ylab="確率") | # ポアソン・ガンマ乱数のグラフ |
| p <- lam/(lam+1) | # 負の二項分布確率パラメータ |
| ynb <- dnbinom(xp, r, p) | # 負の二項分布確率密度 |
| points(xp, ynb, type="b", col="red") | # 負の二項分布のグラフ |
| title(main="ポアソン・ガンマ伝染分布乱数への\n負の二項分布のあてはめ", cex.main=0.8) | |
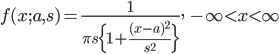
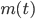 が計算できないので,平均も分散も存在しない.
が計算できないので,平均も分散も存在しない.
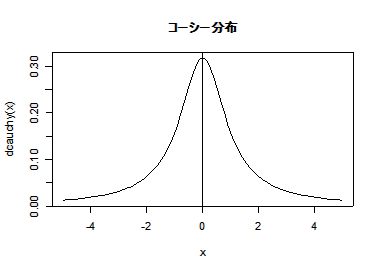
| curve(dcauchy(x), -5, 5) | #コーシー分布の密度関数 |
| abline(v=0, h=0) | # y 軸,x 軸表示 |
| title(main="コーシー分布") | # |
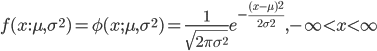
![m(t)={\rm E}[e^{tX}]=e^{t\mu}{\rm E}[e^{t(X-\mu)}]=e^{t\mu} \int^\infty_{-\infty} \frac{1}{\sqrt{2\pi \sigma^2}}e^{t(x-\mu)}e^{-\frac{1}{2\sigma^2}(x-\mu)^2}dx](images/EXTERN_0032.png)
![=e^{t\mu}\frac{1}{\sqrt{2\pi \sigma^2}} \int^\infty_{-\infty}e^{-\frac{1}{2\sigma^2}[(x-\mu)^2-2\sigma^2t(x-\mu)]}dx](images/EXTERN_0033.png)
![=e^{t\mu}\frac{1}{\sqrt{2\pi \sigma^2}} \int^\infty_{-\infty} e^{-\frac{1}{2\sigma^2}[(x-\mu-\sigma^2t)^2-\sigma^4t^2]}dx](images/EXTERN_0034.png)
![{\rm E}[X] = m'(0)=\mu](images/EXTERN_0037.png)
![{\rm Var}[X]={\rm E}[X^2]-({\rm E}[X])^2 = m''(0)-\mu^2 = \sigma^2 +\mu^2-\mu^2 = \sigma^2](images/EXTERN_0038.png)
 |
 |
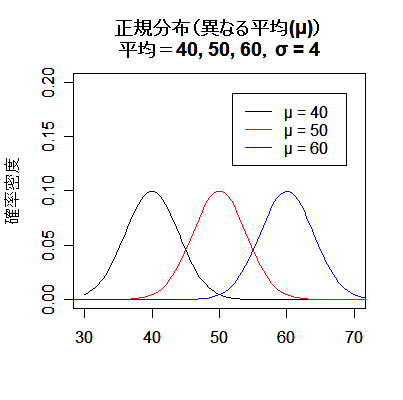
| # 平均の異なる正規分布 | |
| curve(dnorm(x, 40, 4), 30, 70, ylim=c(0,0.2), xlab="",ylab="確率密度") | # 平均:40,標準偏差:4 |
| curve(dnorm(x, 50, 4), add=TRUE, col="red") | # 平均:50,標準偏差:4 |
| curve(dnorm(x, 60, 4), add=TRUE, col="blue") | # 平均:60,標準偏差:4 |
| title(main="正規分布(異なる平均(μ))\n平均=40, 50, 60,σ = 4") | # タイトル |
| legend(52,0.19,c("μ = 40","μ = 50","μ = 60"), lty=1, col=c("black","red","blue")) | # 凡例 |
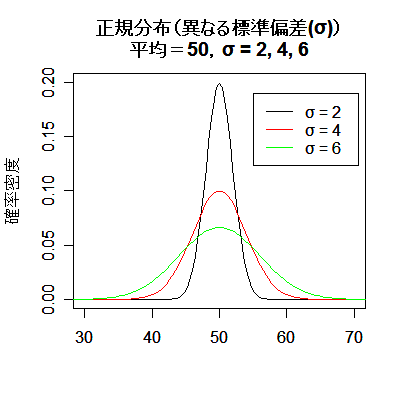
| # 標準偏差(分散)の異なる正規分布 | |
| curve(dnorm(x, 50, sd=2), 30, 70, ylim=c(0,0.2), xlab="",ylab="確率密度") | # 平均:50,標準偏差:2 |
| curve(dnorm(x, mean=50, sd=4), add=TRUE, col="red") | # 平均:50,標準偏差:4 |
| curve(dnorm(x, mean=50, sd=6), add=TRUE, col="green") | # 平均:50,標準偏差:6 |
| title(main="正規分布(異なる標準偏差(σ))\n平均=50,σ = 2, 4, 6") | # タイトル |
| legend(55,0.19,c("σ = 2","σ = 4","σ = 6"), lty=1, col=c("black","red","green")) | # 凡例 |
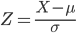
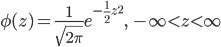
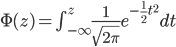
 |
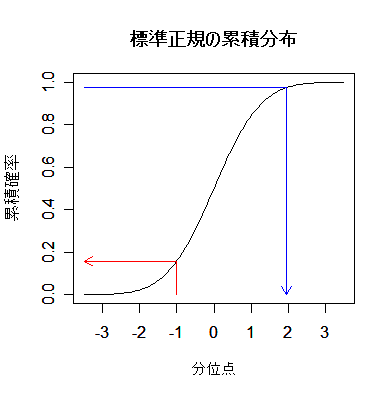 |
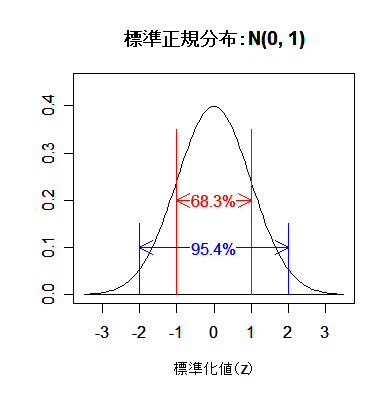
| pnorm(-1) | # = 0.16(赤矢印) |
| pnorm(1) - pnorm(-1) | # = 0.683 |
| pnorm(2) - pnorm(-2) | # = 0.954 |
| qnorm(0.975) | # = 1.96(青矢印),両側 5 %点 |
| 身長 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 |
|---|---|---|---|---|---|---|---|---|---|---|
| 人数 | 2 | 4 | 14 | 41 | 83 | 169 | 394 | 669 | 990 | 1223 |
| 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 |
| 1329 | 1230 | 1063 | 646 | 392 | 202 | 79 | 32 | 16 | 5 | 2 |
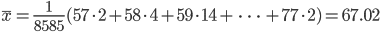 ,
,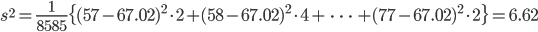 .
.
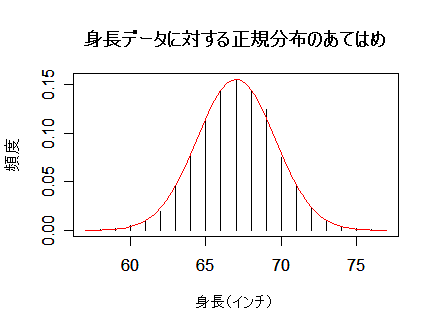
| x <- 57:77 | # 身長(x)の範囲 |
| y <- c(2, 4, 14, 41, 83, 169, 394, 669, 990, 1223, 1329, | # 身長ごとのデータ |
| 1230, 1063, 646, 392, 202, 79, 32, 16, 5, 2) | # |
| s <- sum(y) | # データ総数 |
| m <- sum(x*y/s); m | # データの平均 |
| v <- sum(y/s*(x-m)^2); v | # データの分散 |
| plot(x, y/s, type="h", xlab="身長(インチ)", ylab="頻度") | # データの棒グラフ表示 |
| curve(dnorm(x, m, sqrt(v)), 57, 77, add=T, col="red") | # 正規密度のグラフ表示 |
| title(main="身長データに対する正規分布のあてはめ") | # タイトル |
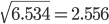 ,と推定される.
,と推定される.
| m <- 67.02; s <- 2.556 | # 平均と標準偏差の指定 |
| 1 - pnorm(70, mean=m, sd=s) | # 1. 70 までの累積確率を 1 から引く |
| qnorm(0.9, mean=m, sd=s) | # 2. 累積確率が 0.9 となる身長 |
| pnorm(70, mean=m, sd=s) - pnorm(65, mean=m, sd=s) | # 3. (70 までの累積確率) - (60 までの累積確率) |
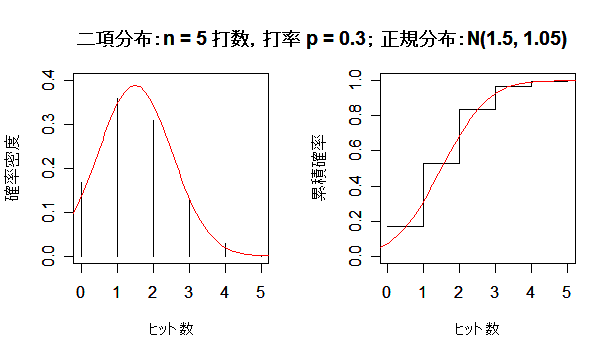

| n <- 5 | # 打数 |
| x <- 0:n | # xの範囲 |
| p <- 0.3 | # 打率 |
| hit <- dbinom(x, size=n, prob=0.3) | # 二項確率 |
| y <- pbinom(x, size=n, prob=0.3) | # 二項累積確率 |
| m <- n*p | # 平均 |
| sd <- sqrt(n*p*(1-p)) | # 標準偏差 |
| op <- par(mfrow = c(1, 2)) | # |
| plot(x, hit, type="h", ylim=c(0,0.4), xlim=c(0,7), xlab="ヒット数", ylab="確率密度") | |
| curve(dnorm(x, mean=m, sd=sd), add=TRUE, col="red") | # 確率密度 |
| plot(x, y, type="s", ylim=c(0,1), xlim=c(0,7), xlab="ヒット数", ylab="累積確率") | |
| curve(pnorm(x, mean=m, sd=sd), add=TRUE, col="red") | # 累積確率 |
| par(op) | # |
| title(main ="二項分布:n = 5 打数,打率 p = 0.3; 正規分布:N(1.5, 1.05) ") | |
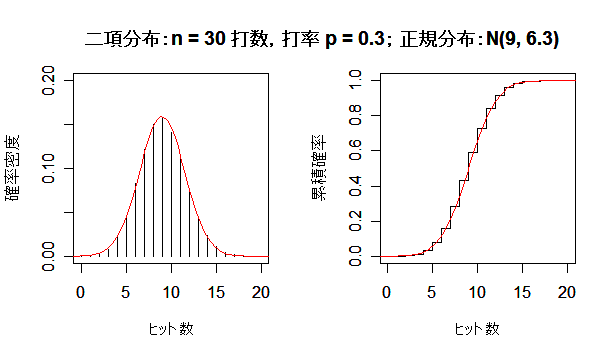
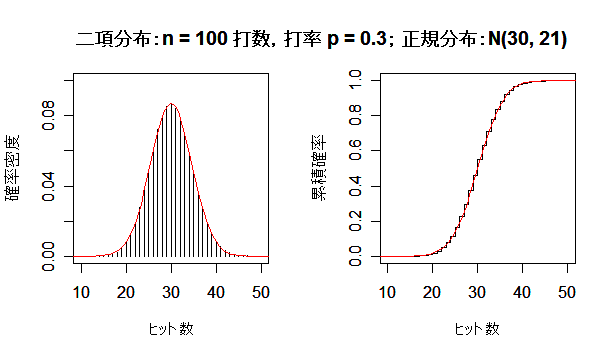
課題:打数 n を大きくして,二項分布が正規分布に近づく様子を確かめよ.
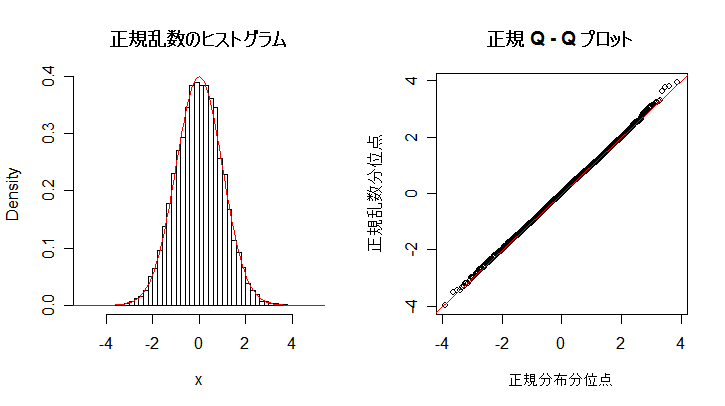
| n <- 10000 | # 乱数列の長さ |
| x <- rnorm(n) | # 標準正規乱数 |
| op <- par(mfrow = c(1, 2)) | # |
| hist(x, breaks=seq(-10,10, by=0.2), xlim=c(-5,5),freq=F, main="") | # 乱数のヒストグラム |
| curve(dnorm(x), add=T, col=2) | # 標準正規分布の重ね合わせ |
| title(main="正規乱数のヒストグラム") | # タイトル |
| qqnorm(x, xlab="正規分布分位点", ylab="正規乱数分位点", main="") | # 正規 Q - Q プロット |
| qqline(x, col=2) | # 正規分布の四分位範囲直線表示 |
| title(main="正規 Q - Q プロット") | # タイトル |
| par(op) | # |
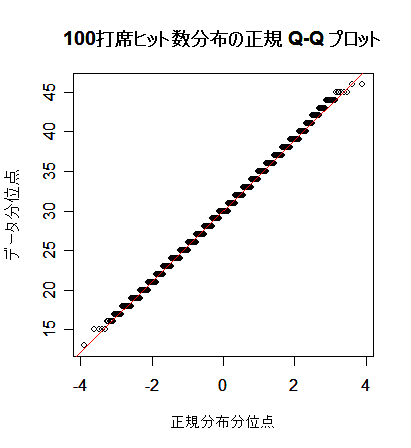
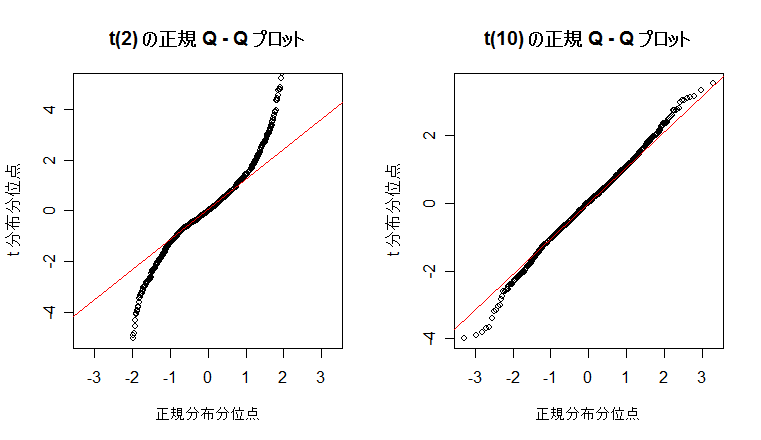
次に,英国人成人身長データと二項分布を正規分布にあてはめた場合について, 正規分布との適合性を正規 Q - Q プロットでみてみよう. 左下図は,身長データの正規 Q - Q プロットで,正規分布から少しずれている様子がわかる. 右下図は,打率 p = 0.3 の選手の n = 100 打席でのヒット数の分布で, 正規分布によくフィットしているのがよくわかる.
 |
 |
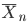 の分布は,
サンプルサイズ n を大きくしていくと平均
の分布は,
サンプルサイズ n を大きくしていくと平均 ![{\rm E}[\bar{X}_n] = \mu](images/EXTERN_0046.png) ,分散
,分散 ![{\rm Var}[\bar{X}_n] = \sigma^2/n](images/EXTERN_0047.png) の正規分布に近づく.
の正規分布に近づく.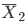 10000個の分布は三角形型をしていて,
正規分布とは似ていない.しかし,10個の標本平均
10000個の分布は三角形型をしていて,
正規分布とは似ていない.しかし,10個の標本平均 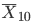 10000個の分布は
正規分布と近づいたが,尾(テイル)の部分のあてはまりは良くない.
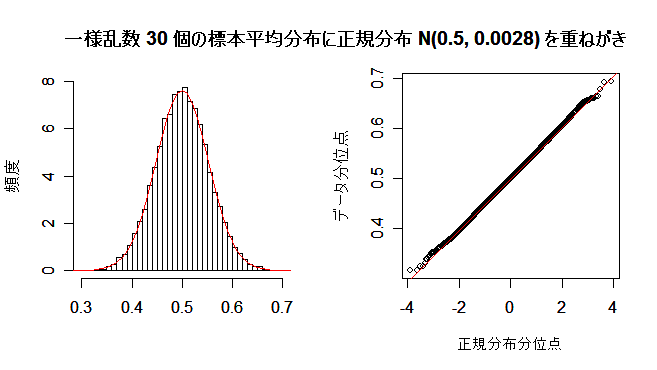
30個の標本平均
10000個の分布は
正規分布と近づいたが,尾(テイル)の部分のあてはまりは良くない.
30個の標本平均 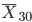 10000個の分布をみると,
尾の部分のあてはまりも改善されてくる.
10000個の分布をみると,
尾の部分のあてはまりも改善されてくる. |
 |
 |
| N <- 10000 | # 乱数列の長さ |
| n <- 2 | # 標本平均のサイズ |
| u <- matrix(data=runif(n*N), ncol=n) | # N×n の一様乱数行列 |
| um <- apply(u, 1, mean) | # 行ごとの平均 |
| op <- par(mfrow = c(1, 2)) | # 標本平均のヒストグラム |
| hist(um, breaks=seq(0,1,by=0.02), freq=FALSE, ylim=c(0, 2.5), xlab="", ylab="頻度", main="") | |
| m <- mean(um) | # 標本平均列の平均 |
| s <- sd(um) | # 標本平均列の標準偏差 |
| curve(dnorm(x, m, s), 0, 1, add=TRUE, col="red") | # 正規分布の重ねがき |
| qqnorm(um, xlab="正規分布分位点", ylab="データ分位点", main="") | # 正規 Q - Q プロット |
| qqline(um, col="red") | # 正規分布の四分位範囲直線表示 |
| par(op) | # |
| title(main="一様乱数 2 個の標本平均分布に正規分布 N(0.5, 0.042) を重ね書き") | |
課題:サンプルサイズ n を大きくして,標本平均の分布が正規分布に近づく様子を確かめよ.
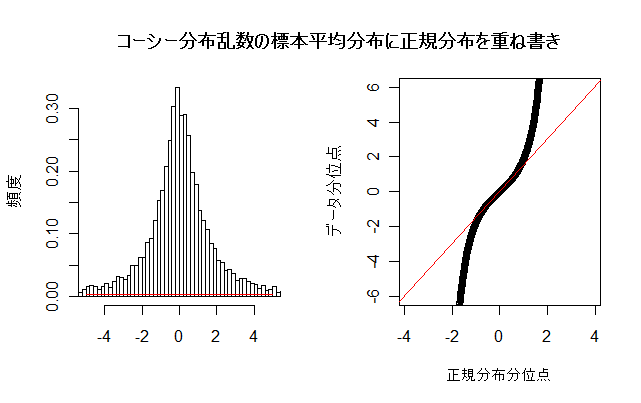
N <- 10000 # 乱数列の長さ n <- 100 # 標本平均のサイズ u <- matrix(data=rcauchy(n*N), ncol=n) # N×n のコーシー分布乱数行列 um <- apply(u, 1, mean) # 行ごとの平均 min(um) # 平均値の最小値 max(um) # 平均値の最大値 uma <- floor(min(um)) umb <- ceiling(max(um)) op <- par(mfrow = c(1, 2)) # 標本平均のヒストグラム hist(um, breaks=seq(uma,umb,by=0.2), xlim=c(-5,5), freq=FALSE, xlab="", ylab="頻度", main="") m <- mean(um); m # 標本平均列の平均 s <- sd(um); s # 標本平均列の標準偏差 curve(dnorm(x, m, s), -5, 5, add=TRUE, col="red") # 正規分布の重ねがき qqnorm(um, xlab="正規分布分位点", ylim=c(-6,6), ylab="データ分位点", main="") # 正規 Q - Q プロット qqline(um, col="red") # 正規分布の四分位範囲直線表示 par(op) title(main="コーシー分布乱数の標本平均分布に正規分布を重ね書き") |
| N <- 10000 | # 点セット列の長さ |
| n <- 1000 | # 乱数点の個数 |
| pi <- NULL | # pi の定義 |
| for(i in 1:N){ | # N 回の繰り返し |
| x <- runif(n, -1, 1) | # (-1, 1) の範囲の一様乱数 n 個生成 |
| y <- runif(n, -1, 1) | # |
| r <- x^2 + y^2 | # 原点からの距離の2乗 |
| pi <- c(pi, 4*length(r[r<1])/n) | # πの近似値ベクトル |
| } | # |
| m = mean(pi) | # 近似値の平均 |
| s = sd(pi) | # 近似値の標準偏差 |
| m | # 平均の表示 |
| s | # 標準偏差の表示 |
| op <- par(mfrow = c(1, 2)) | # |
| hist(pi, freq=F, main="") | # 近似値のヒストグラム |
| curve(dnorm(x, m, s), 2.9, 3.4, add=T, col=2) | # 正規分布の重ね合わせ |
| qqnorm(pi, xlab="正規分布分位点", ylab="データ分位点", main="") | # 正規 Q - Q プロット |
| qqline(pi, col="red") | # 正規分布の直線表示 |
| par(op) | # |
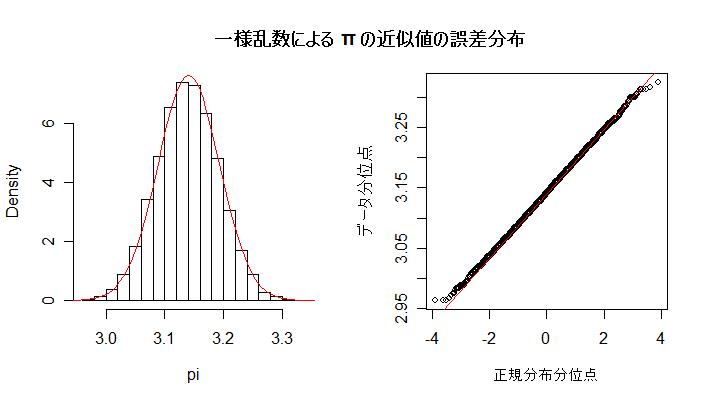
| title(main="一様乱数による π の近似値の誤差分布") | # タイトル |
レポート1:乱数点の個数 n を大きくしたとき,誤差の大きさの減少の程度を n のオーダーで表せ.
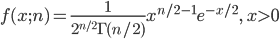
![{\rm E}[X]=as = n/2 \cdot 2 = n,](images/EXTERN_0053.png)
![{\rm Var}[X] = as^2 = n/2 \cdot 4 = 2n](images/EXTERN_0054.png)
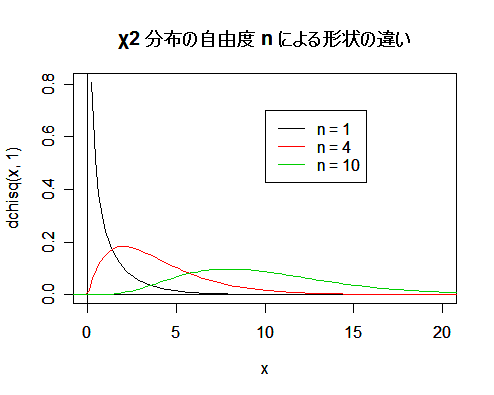
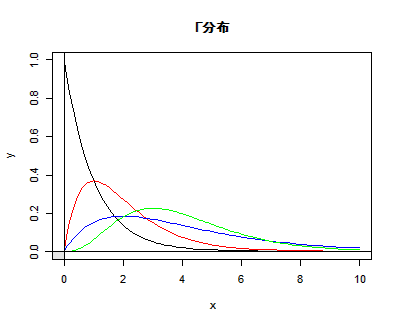
| curve(dchisq(x, 1), 0, 20) | # 自由度 1 の χ2 分布のグラフの表示 |
| abline(v=0, h=0) | # x 軸と y 軸の表示 |
| curve(dchisq(x, 4), add=T, col=2) | # 自由度 4 の χ2 分布のグラフを色 2(赤)で追加 |
| curve(dchisq(x, 10), add=T, col=3) | # 自由度 10 の χ2 分布のグラフを色 3(緑)で追加 |
| legend(10, 0.7, c("n = 1", "n = 4", "n = 10"), lty=1, col=c(1, 2, 3)) | |
| title(main="χ2 分布の自由度 n による形状の違い") | # タイトル |
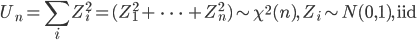
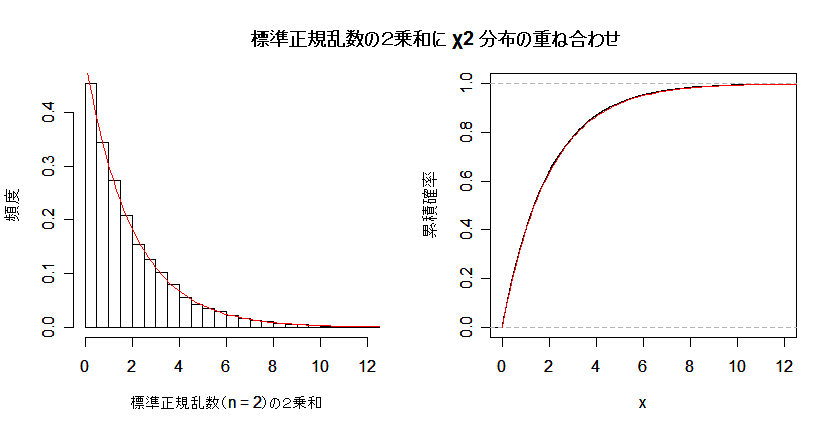
| N <- 10000 | # 乱数列の長さ |
| n <- 2 | # 自由度 |
| u <- matrix(rnorm(n*N), ncol=n) | # N×n の標準正規乱数乱数行列 |
| u2 <- u^2 | # 行列の要素の2乗 |
| un <- apply(u2, 1, sum) | # 行ごとの和 |
| umx <- ceiling(max(un)) | # 最大値を超える整数 |
| op <- par(mfrow = c(1, 2)) | # |
| hist(un, breaks=seq(0,umx,by=0.5), freq=FALSE, xlim=c(0,15), xlab="標準正規乱数(n = 2)の2乗和", ylab="頻度", main="") | |
| curve(dchisq(x, n), 0, 15, add=T, col=2) | # 自由度 2 の χ2 分布の重ね合わせ |
| plot(ecdf(un), do.points=F, verticals=T, xlim=c(0,12), ylab="累積確率", main="") | |
| curve(pchisq(x,2), 0, 15, add=T, col=2) | # 自由度 2 の χ2 累積分布関数の重ね合わせ |
| par(op) | # |
| title(main="標準正規乱数の2乗和に χ2 分布の重ね合わせ") | # タイトル |
課題: 2 乗和する数 n を大きくした場合も,標準正規乱数の 2 乗和の分布が 自由度 n の χ2 分布に従うことを確かめよ.
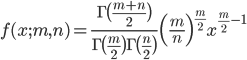
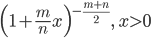
![{\rm E}[X] =\frac{n}{n-2}, \ n>2](images/EXTERN_0058.png)
![{\rm Var}[X]=\frac{2n^2(m+n-2)}{m(n-2)^2(n-4)}, \ n>4](images/EXTERN_0059.png)
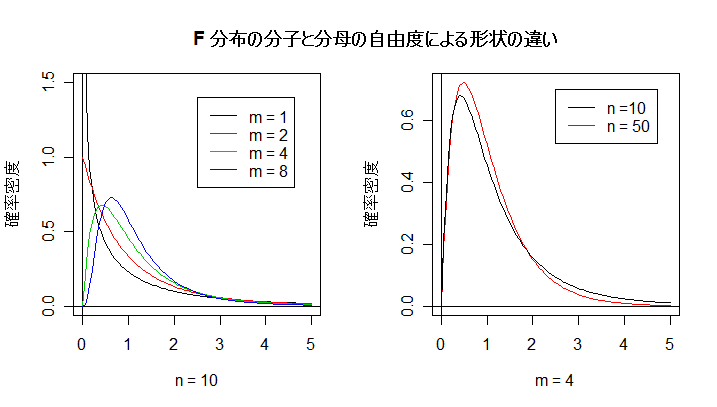
| op <- par(mfrow = c(1, 2)) | # |
| curve(df(x, 1, 10), 0, 5, ylim=c(0,1.5), ylab="確率密度", xlab="n = 10") | # m = 1,n = 10 の F 分布 |
| abline(v=0, h=0) | # x 軸,y 軸 |
| curve(df(x, 2, 10), 0, 5, add=T, col=2) | # m = 2,n = 10 の F 分布 |
| curve(df(x, 4, 10), 0, 5, add=T, col=3) | # m = 4,n = 10 の F 分布 |
| curve(df(x, 8, 10), 0, 5, add=T, col=4) | # m = 8,n = 10 の F 分布 |
| legend(2.5, 1.4, c("m = 1", "m = 2", "m = 4", "m = 8"), lty=1, col=1:4) | # 凡例 |
| curve(df(x, 4, 50), 0, 5, col=2, ylab="確率密度", xlab="m = 4") | # m = 4,n = 50 の F 分布 |
| abline(v=0, h=0) | # x 軸,y 軸 |
| curve(df(x, 4, 10), 0, 5, add=T) | # m = 4,n = 10 の F 分布 |
| legend(2.5, 0.7, c("n =10", "n = 50"), lty=1, col=c("black","red")) | # 凡例 |
| par(op) | # |
| title(main="F 分布の分子と分母の自由度の違いによる形状") | # タイトル |
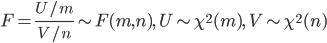
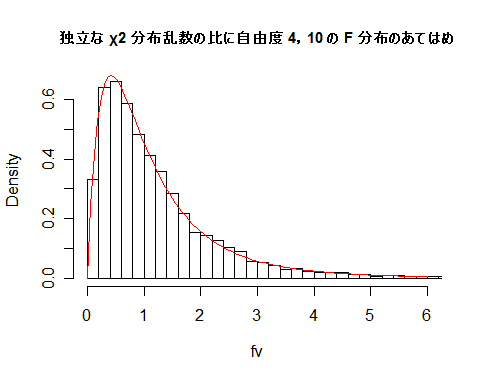
| N <- 10000 | # 乱数列の長さ |
| m <- 4 | # 分子自由度 |
| n <- 10 | # 分母自由度 |
| um0 <- matrix(rnorm(m*N), ncol=m) | # N×m の標準正規乱数乱数行列 |
| um2 <- um0^2 | # 行列の要素の2乗 |
| um <- apply(um2, 1, sum) | # 行ごとの和 |
| um <- um/m | # 自由度で割る |
| un0 <- matrix(rnorm(n*N), ncol=n) | # |
| un2 <- un0^2 | # |
| un <- apply(un2, 1, sum) | # |
| un <- un/n | # |
| fv <- um/un | # χ2 分布乱数の比 |
| fmx <- ceiling(max(fv)) | # fv の最大値を超える整数 |
| hist(fv, breaks=seq(0,fmx,by=0.2), freq=FALSE, xlim=c(0,6), main="") | |
| curve(df(x, m, n), 0, 6, add=T, col=2) | # 自由度 4,10 の F 分布の重ね合わせ |
| title(main="独立な χ2 分布乱数の比に自由度 4,10 の F 分布のあてはめ", cex.main=0.9) | |
課題:分子,分母の自由度を変えて,χ2 分布乱数の比が F 分布に従うことを確かめよ.
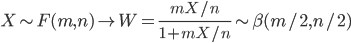
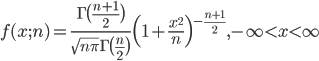
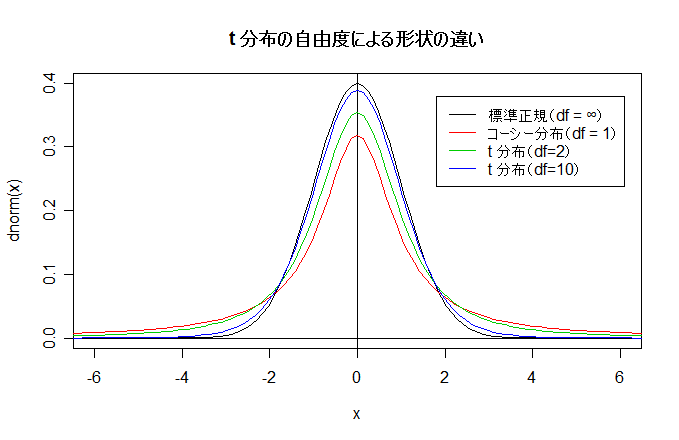
| N <- 10000; n <- 10 | # 乱数列の長さと自由度の設定 |
| y <- rt(N, df=n) | # 自由度 10 の t 分布乱数1000個生成 |
| qqnorm(y, xlab="正規分布分位点", ylab="t 分布分位点", main="") | # 正規 Q - Q プロット |
| qqline(y, col=2) | # 正規分布の四分位範囲直線表示 |
| title(main="t(10) の正規 Q - Q プロット") | # |
課題: 自由度を n の値を変えて,標準正規分布とのずれの様子を正規 Q - Q プロットで確かめよ.
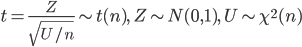
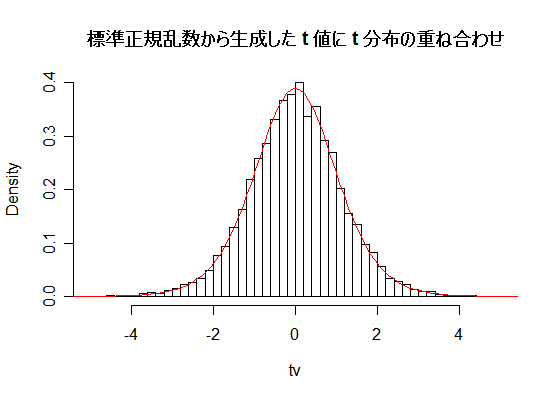
| N <- 10000 | # シミュレーション回数 |
| n <- 10 | # 1回のサンプルサイズ(自由度) |
| un0 <- matrix(rnorm(n*N), ncol=n) | # N×n の標準正規乱数行列 |
| un2 <- un0^2 | # 標準正規乱数行列の要素の2乗 |
| un <- apply(un2, 1, sum) | # 要素の2乗の各行の和(自由度 n の χ2 分布乱数 N 個) |
| unr <- sqrt(un/n) | # 自由度 n の χ2 分布乱数を n で割った平方根 |
| z <- rnorm(N) | # 標準正規乱数 N 個 |
| tv <- z/unr | # t 値 N 個 |
| tmx <- ceiling(max(abs(tv))) | # t 値 の絶対値の最大 |
| hist(tv, breaks=seq(-tmx,tmx,by=0.2), freq=FALSE, xlim=c(-5,5), main="") | |
| curve(dt(x, n), add=T, col=2) | # 自由度 10 の t 分布の重ねがき |
| title(main="標準正規乱数から生成した t 値に t 分布の重ね合わせ") | |