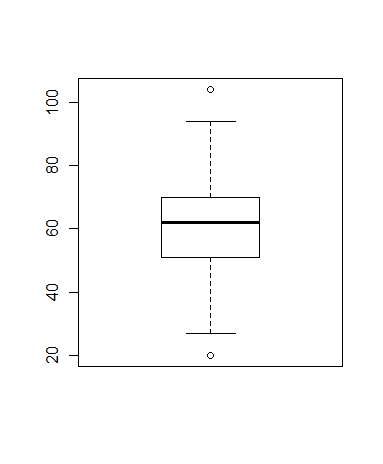東京農工大学
生物統計学演習解答例
問題1:12 人のきょうだい中の女児数のデータ
19 世紀末のドイツの病院のデータによると,同じ両親で 12 人きょうだいがいる 6115 家族の女児数
の数は以下のようであった.
| 女児数 |
0 | 1 |
2 | 3 |
4 | 5 |
6 |
| 度数 |
7 |
45 |
181 |
478 |
829 |
1112 |
1343 |
| 女児数 |
7 |
8 | 9 |
10 | 11 |
12 | 合計 |
| 度数 |
1033 |
670 |
286 |
104 |
24 |
3 | 6115 |
「Weldon のサイコロ実験」と同様な解析を「12人のきょうだい中の女児数のデータ」
に対して行え.
具体的には,Weldon サイコロ実験の解析結果の表のようなものをつくり,結果の解釈を行う.
ヒント:サイコロでは 5 か 6 の目が出る確率は p0 = 1/3 と考えたが,
このデータでは男か女なので p0 = 1/2 である.
- 解答例のスクリプト
-
x <- 0:12 #個数
#dice <- c(185,1149,3265,5475,6114,5194,3067,1331,403,105,18,0,0) #回数データ
dice <- c(7,45,181,478,829,1112,1343,1033,670,286,104,24,3) #女児データ
sum(dice) #試行回数
pdice <- dice/sum(dice) #回数の確率
m <- sum(x*pdice); m #平均
p <- m/12; p #5,6の出る確率
s2 <- sum(pdice*(x-m)^2); s2 #分散
v0 <- 12*0.5*0.5; v0
v <- 12*p*(1-p); v #二項分布のもとでの分散
#h1 <- dbinom(x, 12, 1/3) #正しいサイコロのもとでの二項確率分布
h1 <- dbinom(x, 12, 1/2)
h2 <- dbinom(x, 12, p) #推定確率からの二項確率分布
dicedis <- rbind(pdice,h2,h1) #行ベクトル−>行列
colnames(dicedis) <- as.character(0:12) #列の名前
#barplot(dicedis, beside=TRUE, cex.axis=0.8, cex.lab=1.0, xlab="Number of 5,6", ylab="Probability", legend=c("data","p=0.338", "p=0.333"))
#title(main="Distribution of the experiment of dices by Weldon") #グラフタイトル
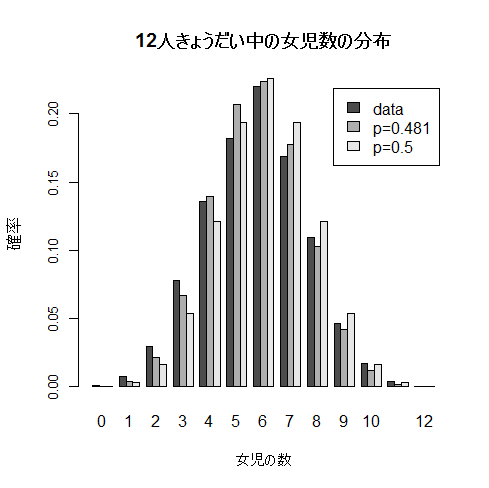
barplot(dicedis, beside=TRUE, cex.axis=0.8, cex.lab=1.0, xlab="女児の数", ylab="確率", legend=c("data","p=0.481", "p=0.5"))
title(main="12人きょうだい中の女児数の分布") #グラフタイトル
12人きょうだい中の女児数の解析結果
| モデル |
平均 | 分散 |
| データ |
5.769 |
3.489 |
| 2項分布(p=0.481) |
5.769 |
2.996 |
| 2項分布(p=0.5) |
6 |
3 |
データはどのモデルもあまり適合していないように見える.男女が独立
であるという前提が成立していないと考えられる.すなわち,男系家系や女系家系
があり単純な二項分布モデルでは現実を捉えることはできないようだ.
問題2:捕獲再捕獲方の推定精度
ここでは捕獲(m = 50),再捕獲(k = 50)合わせて100頭を捕獲している.捕獲総数100頭
を固定して,捕獲頭数と再捕獲頭数を変えたときの推定精度はどうなるか.
また,予算の関係で捕獲総数を半分の50頭にした場合の推定精度はどうなるか.
注)推定精度は,推定値の平均 mv や標準偏差(標準誤差)sd を求め,そこから正規近似により,未知
母数 θ の 95 %信頼区間(Wald 信頼区間)として,
mv - 1.96×sd < θ < mv + 1.96×sd
を出すのが一般的である.
しかし,この例では,推定値が無限大に発散してしまうことがあるので推定値の
平均や標準誤差を求めることができない.このため,シミュレーションにより行った.
推定精度に必要な項目として,推定値の発散割合,メディアン(中央値),90%もしくは95%信頼区間を求める.
ヒント:m = 50,k = 50 のときは,
> m <- 50# 標識をつけた数
> n <- 450# 標識をつけられていない数
> k <- 50# 再捕獲数
> estimate <- NULL# 個体数推定値の定義
> for (i in 1:10000) {# 10000回のシミュレーション
+ x <- rhyper(1, m, n, k)# 超幾何分布に従う乱数1つ抽出
+ estimate <- c(estimate, k * m / x)# 個体数推定値列ベクトル
+ }#
> table(estimate) #推定値の階級分け
estimate
178.571428571429 192.307692307692 208.333333333333 227.272727272727
1 2 14 44
250 277.777777777778 312.5 357.142857142857
122 313 621 1081
416.666666666667 500 625 833.333333333333
1599 1924 1946 1350
1250 2500 Inf
724 212 47
> quantile(estimate, c(0.05, 0.1, 0.5, 0.9, 0.95)) # 分位点(パーセンタイル)
5% 10% 50% 90% 95%
312.5000 312.5000 500.0000 833.3333 1250.0000
となり,真値は 500頭なのに推定頭数が無限大になったケースが 47回あった.無限大に
発散するケースは少ないほどよい.また,推定値分布の分位点から全体のケースのうちの 90%が
312.5 から 1250までの間に含まれていた.この区間の幅が短いほど推定精度がよいことになる.
たとえば,m = 30,k = 70 のときは,
> m <- 30# 標識をつけた数
> n <- 470# 標識をつけられていない数
> k <- 70# 再捕獲数
> estimate <- NULL# 個体数推定値の定義
> for (i in 1:10000) {# 10000回のシミュレーション
+ x <- rhyper(1, m, n, k)# 超幾何分布に従う乱数1つ抽出
+ estimate <- c(estimate, k * m / x)# 個体数推定値列ベクトル
+ }#
> table(estimate) #推定値の階級分け
estimate
150 175 190.909090909091 210
1 1 8 26
233.333333333333 262.5 300 350
116 272 665 1219
420 525 700 1050
1802 2191 1887 1205
2100 Inf
531 76
> quantile(estimate, c(0.05, 0.1, 0.5, 0.9, 0.95)) # 分位点(パーセンタイル)
5% 10% 50% 90% 95%
300 300 525 1050 2100
となり,推定値が無限大に発散したケースは 76回で先ほどより増えた.また,
推定値の 90%区間は,300から2100で,これも先ほどより幅が長くなった.これより,
この組み合わせはよくないことがわかる.
m = 40, k = 60 のときは、
> table(estimate) #推定値の階級分け
estimate
184.615384615385 200 218.181818181818 240
1 12 31 84
266.666666666667 300 342.857142857143 400
214 550 947 1499
480 600 800 1200
1989 1973 1565 787
2400 Inf
297 51
> quantile(estimate, c(0.05, 0.1, 0.5, 0.9, 0.95)) #
5% 10% 50% 90% 95%
300.0000 342.8571 480.0000 1200.0000 1200.0000
>
90%点が1200で大きく、m = 50,k = 50 のときより若干劣る。
m = 60, k = 40 のときは、
> table(estimate) #推定値の階級分け
estimate
184.615384615385 200 218.181818181818 240
2 10 33 98
266.666666666667 300 342.857142857143 400
245 486 1050 1611
480 600 800 1200
1902 1942 1501 799
2400 Inf
280 41
> quantile(estimate, c(0.05, 0.1, 0.5, 0.9, 0.95)) #
5% 10% 50% 90% 95%
300.0000 342.8571 480.0000 1200.0000 1200.0000
Inf が少し減ったが、90%点が1200で大きく、m = 50,k = 50 のときより若干劣る。
捕獲、再捕獲、半々にするのが良いと言える。
捕獲数を半分にして,m = 25,k = 25 のときは
estimate
89.2857142857143 104.166666666667 125 156.25
2 8 50 256
208.333333333333 312.5 625 Inf
954 2372 3682 2676
> quantile(estimate, c(0.05, 0.1, 0.5, 0.9, 0.95)) #
5% 10% 50% 90% 95%
208.3333 208.3333 625.0000 Inf Inf
となり,推定値が無限大に発散したケースは 2676回で1/4に達したので,これでは
調査として成り立たない.すなわち、予算の関係で調査個体を半分にするくらいなら、
調査はやらない方が良い。
問題3:工場労働者の事故数の分布
工場労働者一人当たりの遭遇事故数の分布データ(Greenwood et al. 1920)が以下のようであった.
上のデータをポアソン分布と負の二項分布にあてはめ,どちらの分布のあてはまりがよいか
考察せよ.ただし,'5 以上'は 5 とみなすとする.(正確ではない.)
ヒント:ポアソン分布へのあてはめは,上の死亡記事件数の例と同じである.
負の二項分布へのあてはめは,データの平均と分散が負の二項分布の平均と分散と等しいと考えることにより,
負の二項分布のパラメータの推定ができる.これをモーメント法による分布パラメータの推定という.
なお,負の二項分布の確率密度は dnbinom(x, n, p) で与えられる.
すなわち,データの平均が m,分散が v であったとする.負の二項分布の平均は n(1 - p)/p,
分散は n(1 - p)/p2 であるもで,これらを等しいとおいた連立方程式,
m = n(1 - p)/p, v = n(1 - p)/p2
を解けば負の二項分布のパラメータ n,p の値が m,v で表せる.
- 解答例のスクリプト
-
x <- 0:5 #グラフのx軸の範囲
y <- c(447,132,42,21,3,2) #死亡記事件数データ
s <- sum(y) #データ総数
m <- sum(x*y/s);m #データ分布の平均
v <- sum((x-m)^2*y/s);v #データ分布の分散
yp <- dpois(x, m) #平均 m のポアソン分布確率密度
nbp <- m/v
nbn <- m*nbp/(1-nbp)
ynb <- dnbinom(x, nbn, nbp) # 負の二項分布確率
plot(x, y/s, type="h", ylab="確率") #データの棒グラフ表示
points(x, yp, type="b", col="red") #ポアソン分布の重ねがき(赤)
points(x, ynb, type="b", col="green")
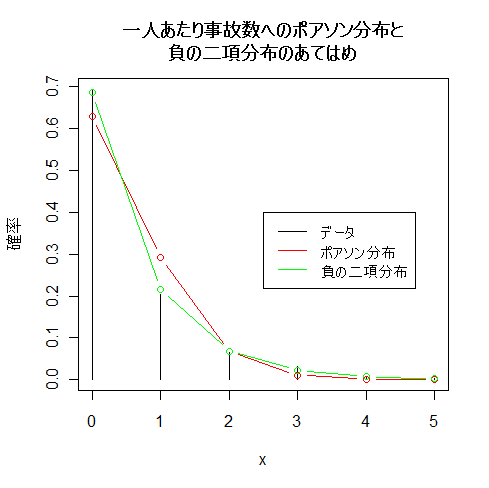
title(main="一人あたり事故数へのポアソン分布と\n負の二項分布のあてはめ")
legend(2.5, 0.4, c("データ", "ポアソン分布", "負の二項分布"), lty=1, col=c("black","red","green"))
ポアソン分布より負の二項分布の方があてはまりがよい.これは,事故を起こす確率がまったく等確率で
はなく,人によって違うことによると考えられる.すなわち,慎重で事故を起こしにくい人と
そそっかしくて事故を起こす確率が高い人がいると考えられる.
問題4:ダイズ地上部乾物重データの正規分布へのあてはめ
長野県中信試験場(現在は,長野県野菜・花卉試験場)で,畦間 75 cm,株間 15 cm で栽培された
ダイズ品種エンレイの個体ごとの地上部
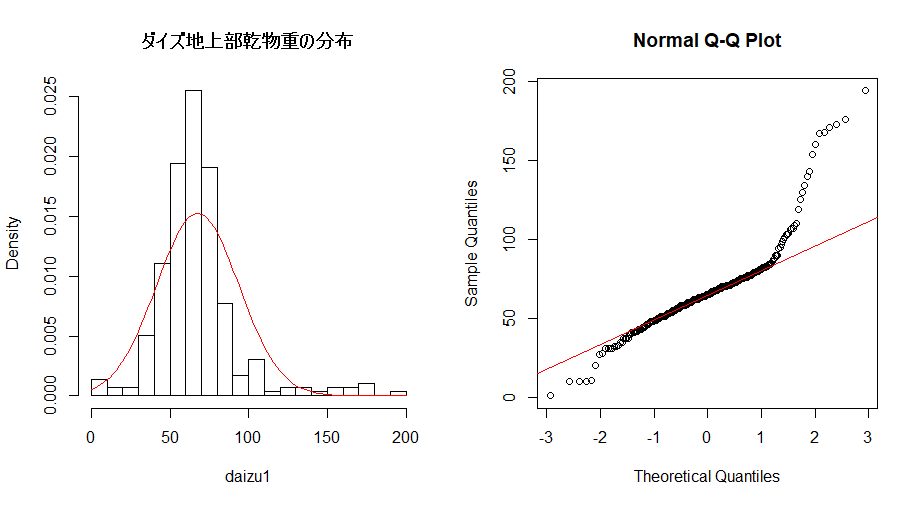
乾物重データを正規分布にあてはめよ.
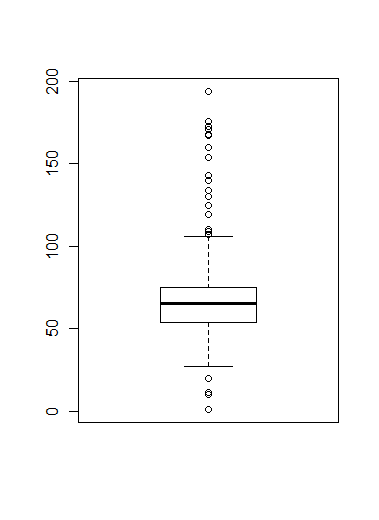
ボックスプロットとデータヒストグラムにあてはめた正規分布を上書きせよ.
夏作物では周辺部分は,隣接個体が少ないことから競合が少なく,また受光や風通し
がよくなったりして圃場内部の個体より生育条件が有利になることがある.これを周辺効果という.
周辺効果の影響を避けるため,圃場実験では周囲の1〜2畦や4〜5株のデータは解析から外すことが多い.
ここで取り上げたデータは,畦1が西側,1行目が北側境界であった.
周辺部分のデータを除き,地上部乾物重データを正規分布にあてはめ,あてはまりの変化を考察せよ.
ヒント:
# "daizu.csv" をデスクトップに保存する.
# ファイルメニューのディレクトリの変更で,作業ディレクトリをデスクトップにする.
daizu <- read.csv("daizu.csv") # データ読み込み.
daizu.mat <- as.matrix(daizu) # daizu はデータフレームなので,行列に変換する.
daizu1 <- as.vector(daizu.mat) # 行列をベクトルデータに変換する.
m1 <- mean(daizu1, na.rm=T) # 欠測値(NA)があるので,これを無視する.
# na.rm=T は NA を remove するのを真 (True) にするという意味.
s1 <- sd(daizu1, na.rm=T)
hist(daizu1, breaks=seq(0, 200, by=10))
daizu2 <- as.vector(daizu.mat[4:25, 4:12]) # 周辺部分である 1 - 3 行目と 1 - 3 列のデータ以外を使う.
m2 <- mean(daizu2, na.rm=T)
s2 <- mean(daizu2, breaks=seq(0, 200, by=10))
hist(daizu2, breaks=seq(0, 200, by=10))
- 解答例のスクリプト
-
dai <- read.csv("daizu.csv"); dai #ダイズ地上部乾物重データ読み込み
dim(dai) #データの大きさ表示
dai[1:10, 1:10] # データの部分表示
height <- as.vector(as.matrix(dai)) #行列データのベクトル化
#
#
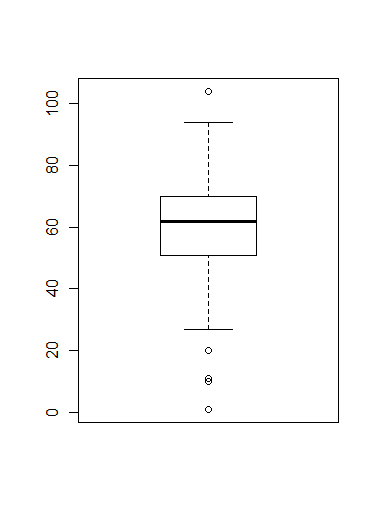
boxplot(height) #箱ヒゲ図
boxplot.stats(height) #箱ひげ図用統計量
#
m <- mean(height, na.rm=TRUE); m #標本平均
s <- sd(height, na.rm=TRUE); s #標本標準偏差
op <- par(mfrow = c(1, 2))
hist(height, breaks=seq(0,200, by=10), freq=FALSE)
curve(dnorm(x, mean=m, sd=s), 0, 200, add=TRUE, col="red") #正規分布
qqnorm(height) #正規 Q - Q プロット
qqline(height, col="red")
par(op)
height2 <- as.vector(as.matrix(dai[4:25, 4:12])) #周辺を除く
boxplot(height2) #箱ヒゲ図
boxplot.stats(height2) #箱ひげ図用統計量
#
m <- mean(height2, na.rm=TRUE); m #標本平均
s <- sd(height2, na.rm=TRUE); s #標本標準偏差
op <- par(mfrow = c(1, 2))
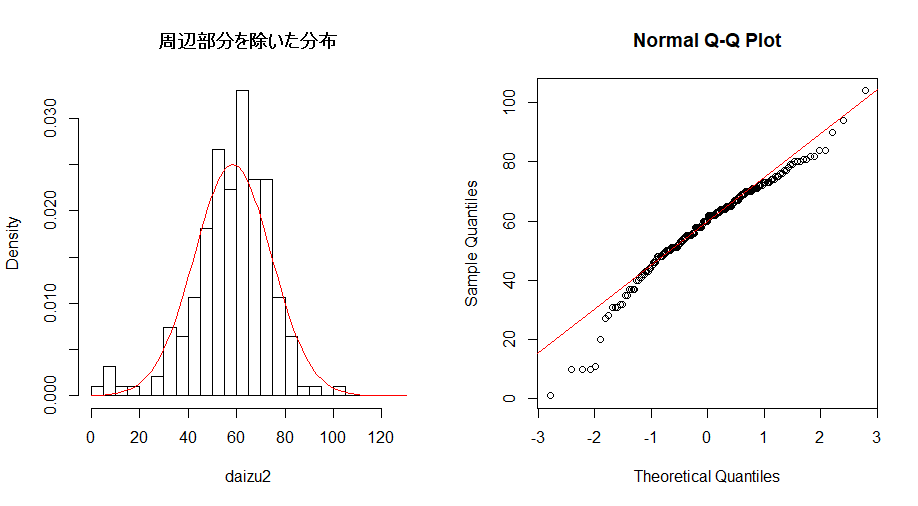
hist(height2, breaks=seq(0,130, by=5), freq=FALSE, main="")
curve(dnorm(x, mean=m, sd=s), 0, 130, add=TRUE, col="red") #正規分布
title(main="周辺部分を除いた分布")
qqnorm(height2) #正規 Q - Q プロット
qqline(height2, col="red")
par(op)
周辺部分を除くと、生育が良すぎた個体が除かれ、確かに周辺効果が存在することが確かめられた。
ところで、この試験はのダイズ個体は1本立てで、NAとなった個体は途中の生育不良で枯死した
個体であった。このため、極端に生育が悪かった個体も、その個体自身の何らかの理由により生育不良
になったものと考えられる。このため、極端に生育の悪い個体(15以下)を用いないで正規分布にあてはめてみた。
height3 <- height2[height2>15] # 特に生育の悪い個体を除く
boxplot(height3) #箱ヒゲ図
boxplot.stats(height3) #箱ひげ図用統計量
m <- mean(height3, na.rm=TRUE); m #標本平均
s <- sd(height3, na.rm=TRUE); s #標本標準偏差
op <- par(mfrow = c(1, 2))
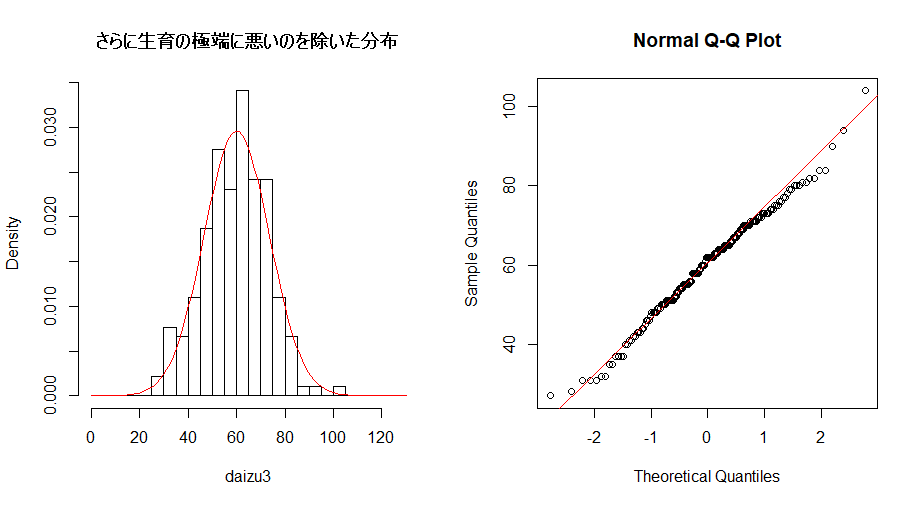
hist(height3, breaks=seq(0,130, by=5), freq=FALSE, main="")
curve(dnorm(x, mean=m, sd=s), 0, 130, add=TRUE, col="red") #正規分布
title(main="さらに生育の極端に悪いのを除いた分布")
qqnorm(height3) #正規 Q - Q プロット
qqline(height3, col="red")
par(op)
正規分布に良く当てはまるようになった。
Copyright (C) 2011, Hiroshi Omori. 最終更新日:2020年10月24日