統計解析ソフトRを用いて,統計解析の理論と実践を学ぶ
1+1 # "#"以降はコメント文で、実行されない。 x <- 3 # "<-" は代入の意味 x x + 5*x # x を用いた演算 # 特別な演算子 5 ^ x # 5の3乗 5 %/% x # 商 5 %% x # 余り # 値の大小の確認 x < 3 # 小なり x <= 3 # 小なりイコール x == 3 # 等しい x != 3 # 等しくない # 種々の数学関数が定義されている。 abs(x) # 絶対値 sqrt(x) # 平方根 sin(x) # sine 正弦 atan(x) # arc tangent 逆正接 log(x) # log e 底eの対数 factorial(x) # x! xの階乗
1:10 # 数列生成 seq(0,1, by=0.05) # 数列生成 rep(1, 5) # 繰り返し rep(1:4, 3) # 繰り返し rep(1:4, each=3) # 繰り返し x <- c(2,-1,3,1) # ベクトル生成 y <- 1:4 x y 2*x + y # ベクトル演算 x * y # 要素同士の積 x / y # 要素同士の割り算 t(x) %*% y # 内積、t()は転置 x %*% t(y) # 行列生成 z <- c(-2,2,-5,-1) a <- cbind(x,y,z); a # 列ベクトル->行列生成 a[2,3] # 要素取り出し a[1,] # 行取り出し a[,1:2] # 2列取り出し a[2:3,2:3] # 部分行列取り出し a[-(1:2),c(1,3)] # 複雑な部分行列取り出し aa <- t(a) %*% a; aa # 行列の積 diag(aa) # 対角成分 solve(aa) # 逆行列 b <- matrix(1:9, nrow=3); b # 行列作成 a %*% b # 行列の積
x1 <- 2; x1 # スカラー代入 x2 <- c(2,-1,3); x2 # ベクトル代入 length(x2) x3 <- matrix(0, nrow=3, ncol=3); x3 # 3*3 の 0 行列 dim(x3) x4 <- array(1:12, dim=c(3,2,2)); x4 # 3*2*2 の配列 dim(x4)
x1 <- "生物統計学"; x1 # 文字列データ
x2 <- c("a", "b", "c"); x2 # 文字列ベクトル
sex <- c("M","F","F","M","F")
age <- c(18,20,19,19,18)
height <- c(170, 165, 160, 180, 170)
weight <- c(62, 48, 50, 68, 60)
major <- c("Math.", "Agr.", "Chem.", "Phys.", "Law")
data <- data.frame(sex, age, height, weight, major)
data
name <- "太郎"
age <- 18
sex <- "M"
score <- c(64, 72, 84, 66, 73)
grade <- c("B", "A", "S", "B", "B", "B")
result <- list("name"=name, "age"=age, "sex"=sex, "score"=score, "grade"=grade)
result
x <- 1:10
y <- c(3,5,6,6,9,10,6,9,10,7)
plot(x, y) # x, y 散布図
reg <- lm(y ~ x) # 回帰の計算
reg$coefficients # 回帰係数
abline(reg, col="red") # 回帰直線の表示
cor(x, y) # 相関係数
title(main="散布図と回帰直線") # グラフタイトル
#
curve(sin(x), 0, 2*pi) # sin カーブ
abline(h=0)
title(main="Graph of sin(x)")
#
#グラフの重ね合わせ
curve(sin(x), 0, 2*pi) # sin カーブ
abline(h=0) # x軸
abline(v=0) # y軸
curve(cos(x), 0, 2*pi, col="red", add=T) # add=T で重ねる。
#
# グラフの重ね合わせ2
x <- seq(0, 2*pi, by=0.01)
plot(x, sin(x), type="l")
lines(x, cos(x), col="red")
abline(h=0)
abline(v=0)
#
# 自作関数のグラフ
# 関数定義
f2 <- function(x){
x*log(x)-x
}
curve(f2(x),0,4) #
abline(h=0)
abline(v=0)
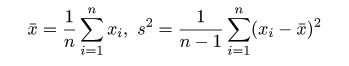
平均とほぼ同様な値としてメディアン(median)(中央値、50%点(percentile)、1/2分位点(1/2 quantile)) がある。データのちらばりの程度は、 25%点(1/4分位点、第一四分位数(1st quartile))と 75%点(3/4分位点、第三四分位数(3rd quartile))の幅である 四分位範囲(interquartile range : IQR)でも測ることができる。
#英語の得点 eigo <- c( 36,70,56,68,76,60,50,63,62,42,64,60,50,68,71,67, 50,65,67,57,72,64,61,66,46,80,46,51,59,32,55,65, 65,52,57,64,23,57,53,54,38,71,57,69,77,61,51,64, 63,43,65,61,51,69,72,68,53,66,68,58,73,65,62,67, 47,81,47,52,59,33,56,66,67,52,58,65,24,58,54,55) length(eigo) #データ数 summary(eigo) # データの要約統計量 mean(eigo) #標本平均 var(eigo) #標本分散 sd(eigo) #標本標準偏差 boxplot(eigo, main="英語得点の箱ヒゲ図") #箱ひげ図 boxplot.stats(eigo) #箱ひげ図用統計量 hist(eigo, breaks=seq(0, 100, by=5), xlab="英語得点", ylab="頻度", main="") title(main = "英語得点のヒストグラム") #グラフタイトル stem(eigo, scale=2) #幹葉表示
#ダイズデータ読み込み
daizu.df <- read.csv("daizu.csv") # daizu.csv ファイル読み込み
dim(daizu.df) # データの大きさ
head(daizu.df) # 最初の一部の行のみを表示
#daizu.dfはdata.frameなので行列に変換する。
daizu.mat <- as.matrix(daizu.df)
# その後ベクトル化して1次元数値データにする。
daizu <- as.vector(daizu.mat)
length(daizu)
summary(daizu)
#データに欠測値、NA(Not Avairable) が含まれていると計算してくれないので、
#NA部分を除く(remove)という命令、na.rm=Tを付け加える必要がある。
mean(daizu)
mean(daizu, na.rm=T)
sd(daizu, na.rm=T)
#ダイズデータをグラフにする。
boxplot(daizu)
hist(daizu, breaks=seq(0, 200, by=5))
rowmean <- apply(daizu.df, 1, mean, na.rm=T); rowmean # 行平均 colmean <- apply(daizu.df, 2, mean, na.rm=T); colmean # 列平均 plot(rowmean, type="b") plot(colmean, type="b")
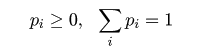
| X | 0 | 1 | 2 | … |
| P | p0 | p1 | p2 | … |
| X | 0 | 1 |
| P | 1/2 | 1/2 |
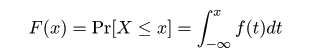
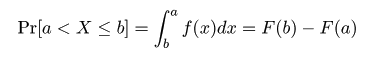
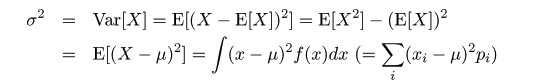
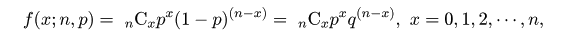
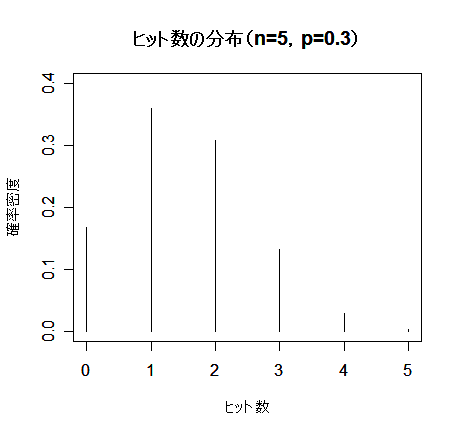
| n <- 5 | #試行回数 |
| x <- 0:n | #回数 |
| p <- 0.3 | #成功確率 |
| hit <- dbinom(x, size=n, prob=0.3) | #二項確率 |
| plot(x, hit, type="h", ylim=c(0,0.4), xlim=c(0,n), cex.lab=0.8, xlab="ヒット数", ylab="確率密度") | |
| title(main="ヒット数の分布(n=5,p=0.3)") | #タイトル |
| sum(x*hit) | #平均(np = 1.5) |
| sum(hit*(x - n*p)^2) | #分散(np(1 - p) = 1.05) |
| 5,6の個数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 出た回数 | 185 | 1149 | 3265 | 5475 | 6114 | 5194 | 3067 |
| 5,6の個数 | 7 | 8 | 9 | 10 | 11 | 12 | 合計 |
| 出た回数 | 1331 | 403 | 105 | 18 | 0 | 0 | 26306 |
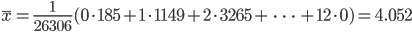 ,
,
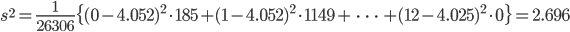
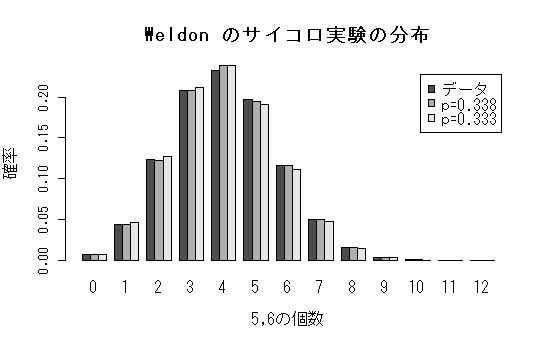
1つのサイコロが 5 か 6 の目を出す確率を p とすると,12個のサイコロを同時に振って,5 か 6 の目
が出る個数は 2 項分布 B(12, p) に従うはずである.
2 項分布 B(12, p) の平均は 12p,分散は 12p(1-p) であるので,
p のデータからの
推定値p^は,データの平均値を用いて,

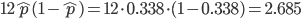
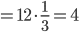 ,
分散
,
分散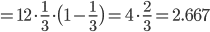
| モデル | 平均 | 分散 |
|---|---|---|
| データ | 4.052 | 2.696 |
| 2項分布(p=0.338) | 4.052 | 2.685 |
| 2項分布(p=0.333) | 4 | 2.667 |
| x <- 0:12 | #個数 |
| dice <- c(185,1149,3265,5475,6114,5194,3067,1331,403,105,18,0,0) | #回数データ |
| sum(dice) | #試行回数 |
| pdice <- dice/sum(dice) | #回数の確率 |
| m <- sum(x*pdice); m | #平均 |
| p <- m/12 | #5,6の出る確率 |
| s2 <- sum(pdice*(x-m)^2); s2 | #分散 |
| v <- 12*p*(1-p) | #二項分布のもとでの分散 |
| h1 <- dbinom(x, 12, 1/3) | #正しいサイコロのもとでの二項確率分布 |
| h2 <- dbinom(x, 12, p) | #推定確率からの二項確率分布 |
| dicedis <- rbind(pdice,h2,h1) | #行ベクトル->行列 |
| colnames(dicedis) <- as.character(0:12) | #列の名前 |
| barplot(dicedis, beside=TRUE, cex.axis=0.8, cex.lab=1.0, xlab="Number of 5,6", ylab="Probability", legend=c("data","p=0.338", "p=0.333")) | |
| title(main="Distribution of the experiment of dices by Weldon") | #グラフタイトル |
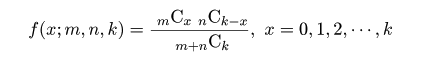
| x <- 0:20 | # 抽出された白石の個数 |
| m <- 50 | # 白石の個数 |
| n <- 450 | # 黒石の個数 |
| k <- 50 | # 抽出回数 |
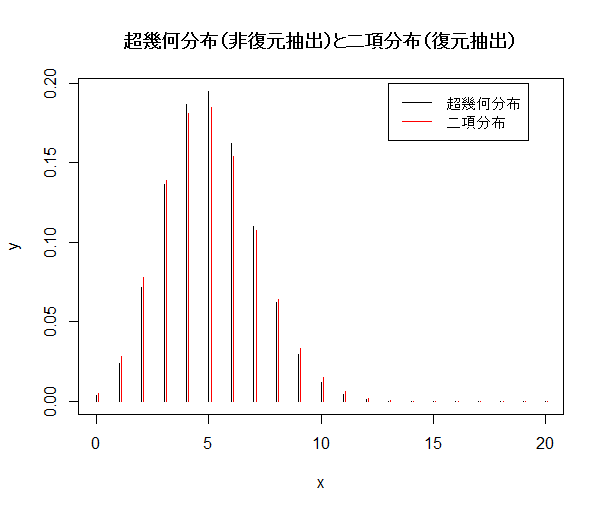
| y <- dhyper(x, m, n, k) | # 超幾何分布確率分布 |
| plot(x,y,type="h") | # |
| p <- m/(m+n) | # 白石が選ばれる確率 |
| yd <- dbinom(x, k, p) | # 二項確率 |
| x1 <- x+0.1 | # 0.1 ずらして表示 |
| points(x1, yd, type="h", col="red") | # 二項確率のグラフ |
| title(main="超幾何分布(非復元抽出)と二項分布(復元抽出)") | # |
| legend(13,0.2,legend=c("超幾何分布","二項分布"), lty=1, col=c("black", "red")) | |
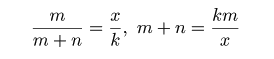
| m <- 50 | # 標識をつけた数 |
| n <- 450 | # 標識をつけられていない数 |
| k <- 50 | # 再捕獲数 |
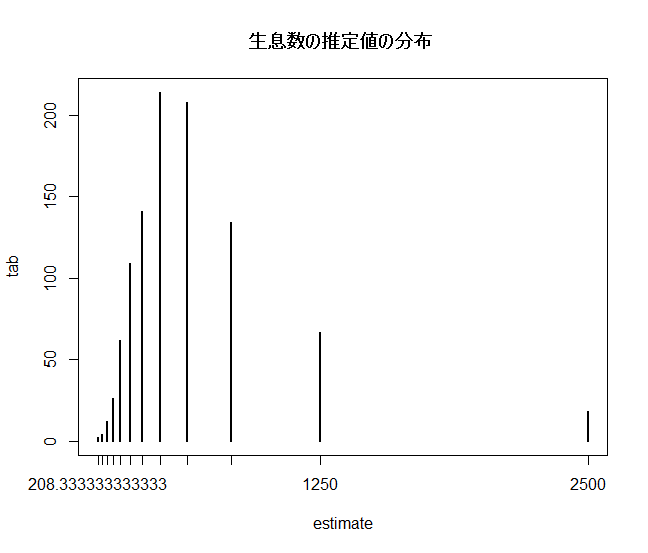
| x <- rhyper(1000, m, n, k) | # 超幾何分布に従う乱数1000抽出 |
| estimate <- k * m / x | # 個体数推定値列ベクトル |
| tab <- table(estimate); tab | #推定値の階級分け |
| plot(tab) | #グラフ |
| title(main="生息数の推定値の分布 ") | #タイトル |
| quantile(estimate, c(0.05, 0.1, 0.5, 0.9, 0.95)) | # 分位点(パーセンタイル) |
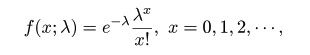
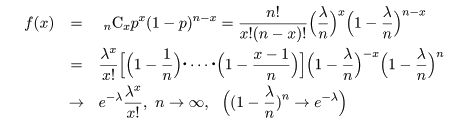
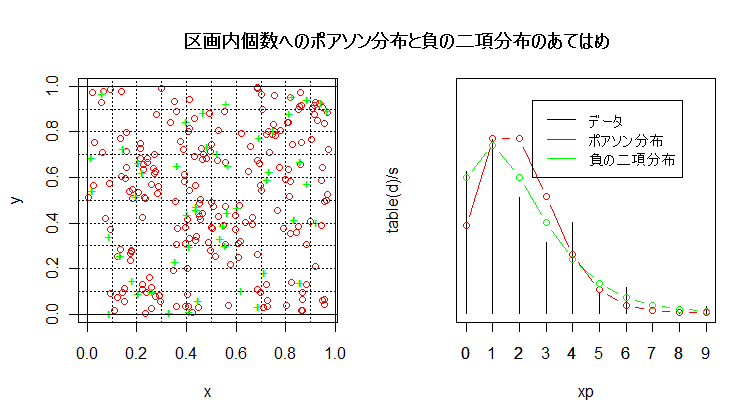
となり,n の極限でこの二項分布は平均 λ のポアソン分布に従うことがわかる.
| 死亡記事件数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 以上 |
|---|---|---|---|---|---|---|---|
| 日数 | 484 | 391 | 164 | 45 | 11 | 1 | 0 |
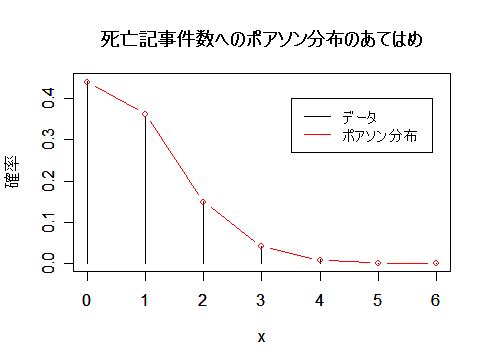
死亡記事件数データの平均は0.8239,分散は0.8294,であった.このデータがポアソン分布に従っている
と考える.ポアソン分布の平均は λ なので,λ = 0.8239 のポアソン分布にあてはめてみたところ,非常によく
一致していた.
また,ポアソン分布は,平均と分散が等しいという特徴がある.データの平均と分散の値が
近いことから,データはポアソン分布によく適合していることを示している.
 |
|
| x <- 0:6 | #グラフのx軸の範囲 |
| y <- c(484, 391, 164, 45, 11, 1, 0) | #死亡記事件数データ |
| s <- sum(y) | #データ総数 |
| m <- sum(x*y/s) | #データ分布の平均 |
| v <- sum((x-m)^2*y/s) | #データ分布の分散 |
| yp <- dpois(x, m) | #平均 m のポアソン分布確率密度 |
| plot(x, y/s, type="h", ylab="確率") | #データの棒グラフ表示 |
| points(x, yp, type="b", col="red") | #ポアソン分布の重ねがき(赤) |
| title(main="死亡記事件数へのポアソン分布のあてはめ") | |
| legend(3.5, 0.4, c("データ", "ポアソン分布"), lty=1, col=c("black","red")) | |
| n <- 200 | # 個体数 |
| m <- 10 | # メッシュ(m2 個) |
| x <- runif(n) | # 一様乱数n個 |
| y <- runif(n) | # 一様乱数n個 |
| # | # |
| count <- NULL | # count の定義 |
| for(i in 1:m){ | # m 回の繰り返し |
| n1 <- (1:n)[x < (i-1)/m] | # (i-1)/m 以下の乱数である番号 |
| n2 <- (1:n)[x < i/m] | # i/m 以下の乱数である番号 |
| nin <- n2[!n2 %in% n1] | # (i-1)/m から i/m の番号 |
| yy <- y[nin] | # 上記 x 座標に対する y 座標 |
| a <- hist(yy, breaks=0:m/m) | # yy を 0 から 1 まで 1/m きざみで区切る |
| count <- c(count, a$counts) | # 区切った領域に入った個体の個数のベクトル |
| } | # 繰り返しここまで |
| mc <- max(count) | # メッシュ内の個数の最大値 |
| xp <- 0:mc | # 個数の定義域 |
| d <- factor(count, levels=xp) | # 個数が 0 の階級も含める |
| table(d) | # メッシュ内個数の区分 |
| s <- sum(table(d)) | # 総個数 |
| m1 <- sum(xp*table(d)/s) | # カウント分布の平均 |
| m2 <- mean(count) | # カウントデータの標本平均 |
| v1 <- sum(table(d)/s*(xp-m1)^2) | # カウント分布の分散 |
| v2 <- var(count) | # カウントデータの標本分散 |
| # | # |
| op <- par(mfrow = c(1, 2)) | # 横に2つのグラフを並べる |
| plot(x,y, col="red") | # 個体分布の表示 |
| abline(h=0, v=0) | # 外枠 |
| abline(h=1, v=1) | # 外枠 |
| for(i in 1:m) abline(h=i/m, v=i/m, lty=2) | # メッシュ区分線 |
| plot(xp, table(d)/s, type="h") | # 区分された分布のグラフ |
| lam <- n/(m*m) | # 平均 |
| yp <- dpois(xp, lam) | # ポアソン分布確率密度 |
| points(xp, yp, type="b", col="red") | # ポアソン分布グラフ表示 |
| par(op) | # グラフ表示もとに戻す |
| title(main="Distribution of number of individuals in mesh partitions") | # タイトル |
| m1 | # カウント分布平均 |
| v1 | # カウント分布分散 |
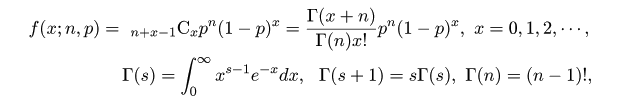
n <- 200 # 個体数(予定)
m <- 10 # メッシュ(m2 個)
p <- 4 # 平均子ども数
sig <- 0.05 # 正規分布標準偏差
xx <- NULL # xx(子ども座標)の定義
xx0 <- NULL # xx0(親座標)の定義
np <- round(n/p) # 親の数(round() は 5 捨 6 入)
for(i in 1:np){ # np 回の繰り返し
x0 <- runif(2) # 親個体の座標を一様乱数で生成
n0 <- rpois(1, p) # 子どもの数を平均 p のポアソン乱数で生成
for(j in 1:n0){ # n0 回の繰り返し
xd <- rnorm(2, m=x0, sd=sig) # 子どもの座標を,正規乱数 N(x0, sig2)で生成
if(xd[1] > 1) xd[1] <- xd[1] - 1 # x 座標が 1 を超えたとき区画の左端に
if(xd[1] < 0) xd[1] <- xd[1] + 1 # x 座標が 0 未満のとき区画の右端に
if(xd[2] > 1) xd[2] <- xd[2] - 1 # y 座標が 1 を超えたとき区画の下辺に
if(xd[2] < 0) xd[2] <- xd[2] + 1 # y 座標が 0 未満のとき区画の上辺に
xx <- rbind(xx, xd) # 個体座標行列の行の追加
xx0 <- rbind(xx0, x0) # 個体座標行列の行の追加
} #
} #
# 区画内個体数 #
x <- xx[,1]; y <- xx[,2] # x 座標ベクトル,y 座標ベクトル
count <- NULL # count の定義
for(i in 1:m){ # m 回の繰り返し
n1 <- (1:n)[x < (i-1)/m] # (i-1)/m 以下の乱数である番号
n2 <- (1:n)[x < i/m] # i/m 以下の乱数である番号
nin <- n2[!n2 %in% n1] # (i-1)/m から i/m の番号
yy <- y[nin] # 上記 x 座標に対する y 座標
a <- hist(yy, breaks=0:m/m) # yy を 0 から 1 まで 1/m きざみで区切る
count <- c(count, a$counts) # 区切った領域に入った個体の個数のベクトル
} #
mc <- max(count) # メッシュ内の個数の最大値
xp <- 0:mc # 個数の定義域
d <- factor(count, levels=xp) # 個数が 0 の階級も含める
table(d) # メッシュ内個数の階級区分
s <- sum(table(d)) # 総個体数
m1 <- sum(xp*table(d)/s) # カウント分布の平均
v1 <- sum(table(d)/s*(xp-m1)^2) # カウント分布の分散
# #
op <- par(mfrow = c(1, 2)) # 横に2つのグラフを並べる
plot(x,y, col="red") # 個体分布の表示
points(xx0, pch="+", col="green") # 個体分布の表示
abline(h=0, v=0) # 外枠
abline(h=1, v=1) # 外枠
for(i in 1:m) abline(h=i/m, v=i/m, lty=3) # メッシュ区分線
plot(xp, table(d)/s, type="h", ylim=c(0,0.35)) # 区分された分布のグラフ
yp <- dpois(xp, m1) # ポアソン分布確率
points(xp, yp, type="b", col="red") # ポアソン分布表示
nbp <- m1/v1 #
nbn <- m1*nbp/(1-nbp) #
ynb <- dnbinom(xp, nbn, nbp) # 負の二項分布確率
points(xp, ynb, type="b", col="green") # 負の二項分布表示
legend(2.5, 0.33, c("データ", "ポアソン分布", "負の二項分布"), lty=1, col=c("black","red","green"))
par(op) # 個体数
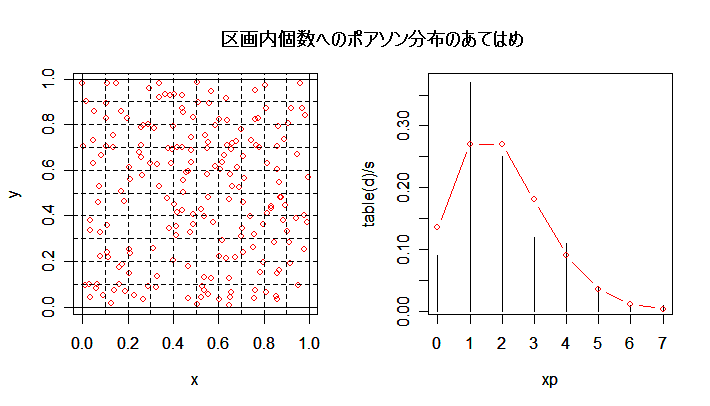
title(main="区画内個数へのポアソン分布と負の二項分布のあてはめ")
m1 # 平均
v1 # 分散
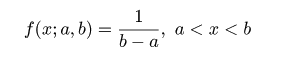
平均: E[X ] = (a + b)/2,
分散: Var[X ] = (b - a)2/12
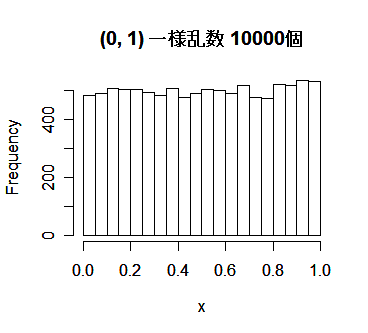
| x <- runif(10000) | #(0,1)一様乱数1000個列 |
| hist(x, main="(0, 1) 一様乱数 10000個") | #ヒストグラム表示 |
| mean(x) | # 一様乱数の平均(理論値は 1/2) |
| var(x) | # 一様乱数の分散 (理論値は 1/12) |
| n <- 10000 | #一様乱数の個数 |
| x <- runif(n, -1, 1) | #(-1, 1) の範囲の一様乱数 n 個生成 |
| y <- runif(n, -1, 1) | # |
| r <- x^2 + y^2 | #原点からの距離の2乗 |
| plot(x,y, type="n", xlim=c(-1,1), ylim=c(-1,1)) | #グラフの表示範囲の指定 |
| abline(h=0) | # x 軸の表示 |
| abline(v=0) | # y 軸の表示 |
| segments(-1, 1, 1, 1) | #(-1, 1)から(1, 1)までの直線 |
| segments(1, 1, 1, -1) | # |
| segments(-1, -1, 1, -1) | # |
| segments(-1, -1, -1, 1) | # |
| pin <- (1:n)[r<1] | #乱数のうち単位円内に入る乱数の番号 |
| points(x[-pin], y[-pin], pch=".", col="green") | #単位円の外の乱数を緑点で表示 |
| points(x[pin], y[pin], pch=".", col="red") | #単位円内の乱数を赤い点で表示 |
| s <- 0:360 | # 0 度から 360 度 |
| theta <- s*pi/180 | #度をラジアンに変換 |
| xp = sin(theta) | #単位円の x 座標 |
| yp = cos(theta) | #単位円の y 座標 |
| points(xp,yp, type="l") | #単位円を表示 |
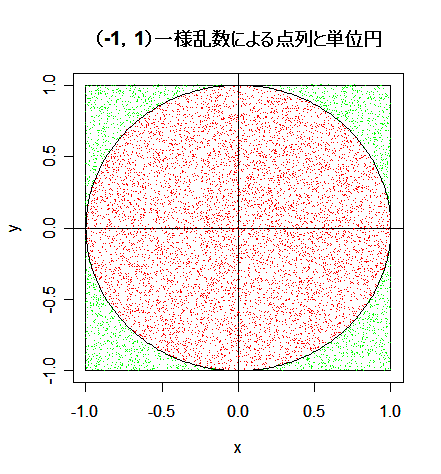
| title(main="(-1,1)一様乱数による点列と単位円") | |
| length(pin) | #単位円内に入った乱数の個数 |
| 4*length(pin)/n | #πの近似値 |
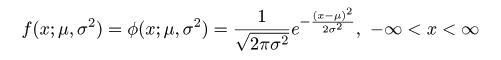
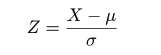
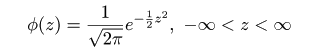
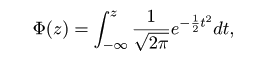
 |
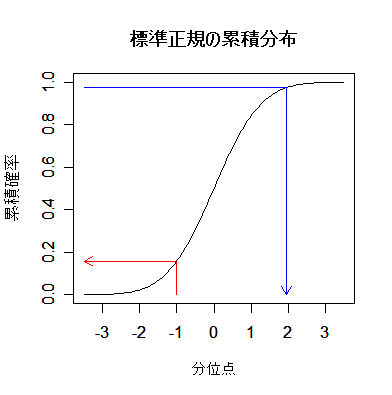 |
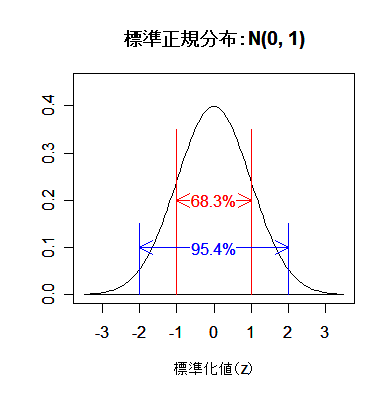
| pnorm(-1) | # = 0.16(赤矢印) |
| pnorm(1) - pnorm(-1) | # = 0.683 |
| pnorm(2) - pnorm(-2) | # = 0.954 |
| qnorm(0.975) | # = 1.96(青矢印),両側 5 %点 |
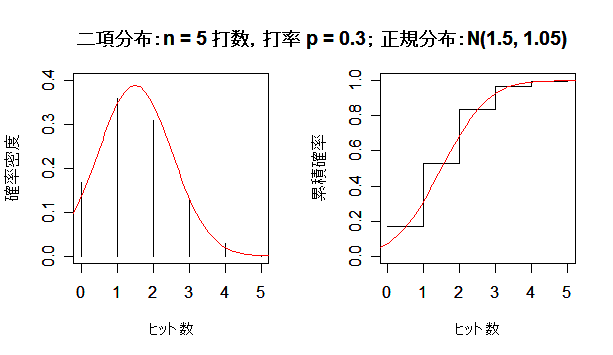
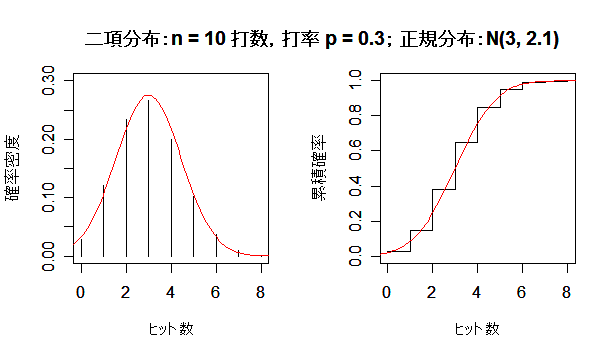
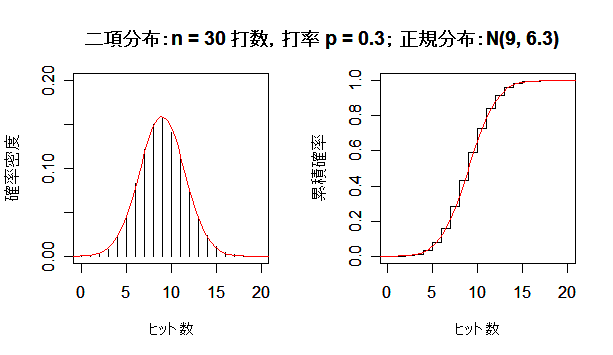
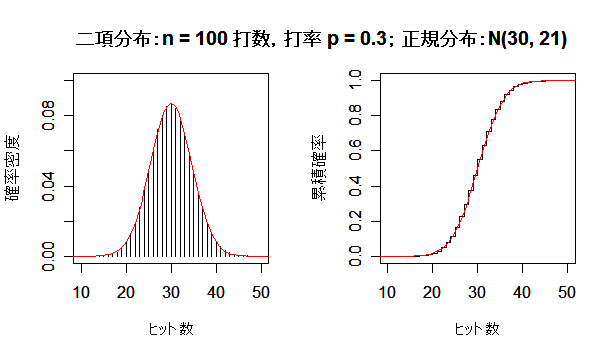
| n <- 5 | # 打数 |
| x <- 0:n | # xの範囲 |
| p <- 0.3 | # 打率 |
| hit <- dbinom(x, size=n, prob=0.3) | # 二項確率 |
| y <- pbinom(x, size=n, prob=0.3) | # 二項累積確率 |
| m <- n*p | # 平均 |
| sd <- sqrt(n*p*(1-p)) | # 標準偏差 |
| op <- par(mfrow = c(1, 2)) | # |
| plot(x, hit, type="h", ylim=c(0,0.4), xlim=c(0,7), xlab="ヒット数", ylab="確率密度") | |
| curve(dnorm(x, mean=m, sd=sd), add=TRUE, col="red") | # 確率密度 |
| plot(x, y, type="s", ylim=c(0,1), xlim=c(0,7), xlab="ヒット数", ylab="累積確率") | |
| curve(pnorm(x, mean=m, sd=sd), add=TRUE, col="red") | # 累積確率 |
| par(op) | # |
| title(main ="二項分布:n = 5 打数,打率 p = 0.3; 正規分布:N(1.5, 1.05) ") | |
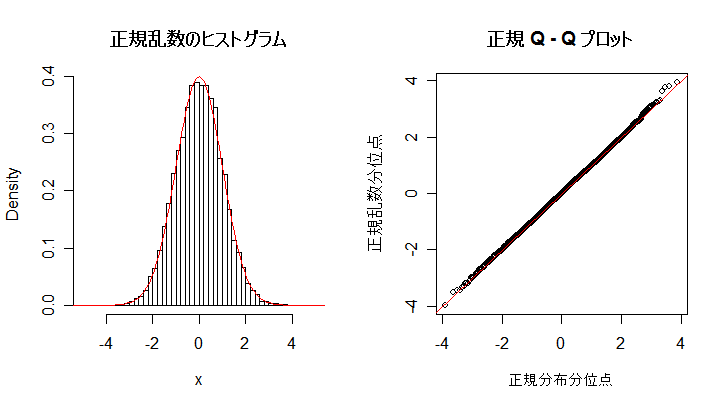
| n <- 1000 | # 乱数列の長さ |
| x <- rnorm(n) | # 標準正規乱数 |
| op <- par(mfrow = c(1, 2)) | # |
| hist(x, breaks=seq(-10,10, by=0.2), xlim=c(-5,5),freq=F, main="") | # 乱数のヒストグラム |
| curve(dnorm(x), add=T, col=2) | # 標準正規分布の重ね合わせ |
| title(main="Histgram of Normal random numbers") | # タイトル |
| qqnorm(x, main="") | # 正規 Q - Q プロット |
| qqline(x, col=2) | # 正規分布の四分位範囲直線表示 |
| title(main="Normal Q - Q plot") | # タイトル |
| par(op) | # |
 |
 |
 |
| N <- 10000 | # 乱数列の長さ |
| n <- 2 | # 標本平均のサイズ |
| u <- matrix(data=runif(n*N), ncol=n) | # N×n の一様乱数行列 |
| um <- apply(u, 1, mean) | # 行ごとの平均 |
| op <- par(mfrow = c(1, 2)) | # 標本平均のヒストグラム |
| hist(um, breaks=seq(0,1,by=0.02), freq=FALSE, ylim=c(0, 2.5), xlab="", ylab="頻度", main="") | |
| m <- mean(um) | # 標本平均列の平均 |
| s <- sd(um) | # 標本平均列の標準偏差 |
| curve(dnorm(x, m, s), 0, 1, add=TRUE, col="red") | # 正規分布の重ねがき |
| qqnorm(um, xlab="正規分布分位点", ylab="データ分位点", main="") | # 正規 Q - Q プロット |
| qqline(um, col="red") | # 正規分布の直線表示 |
| par(op) | # |
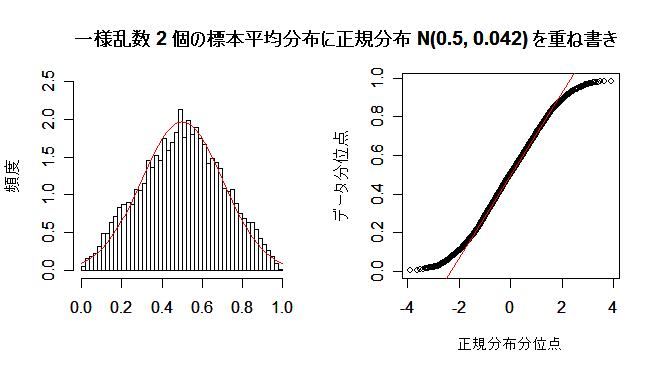
| title(main="一様乱数 2 個の標本平均分布に正規分布 N(0.5, 0.042) を重ね書き") | |
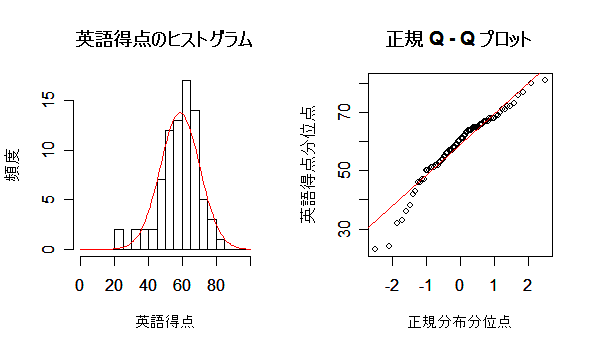
eigo <- c( 36,70,56,68,76,60,50,63,62,42,64,60,50,68,71,67, # 英語得点データ 50,65,67,57,72,64,61,66,46,80,46,51,59,32,55,65, 65,52,57,64,23,57,53,54,38,71,57,69,77,61,51,64, 63,43,65,61,51,69,72,68,53,66,68,58,73,65,62,67, 47,81,47,52,59,33,56,66,67,52,58,65,24,58,54,55) d <- 5 # ヒストグラムの階級幅 n <- length(eigo) # データ数 m <- mean(eigo) # 平均 s <- sd(eigo) # 標準偏差 op <- par(mfrow = c(1, 2)) # グラフを横に2つ並べて表示 hist(eigo, breaks=seq(0, 100, by=d), freq=F, xlab="英語得点", ylab="密度", main="") # 密度ヒストグラム curve(dnorm(x, m, s), 0, 100, add=TRUE, col="red") # 推定正規分布重ねて表示 title(main="英語得点のヒストグラム") # qqnorm(eigo, xlab="正規分布分位点", ylab="英語得点分位点", main="") qqline(eigo, col=2) # Q-Q プロット title(main="正規 Q - Q プロット") # par(op) |
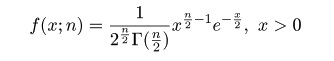
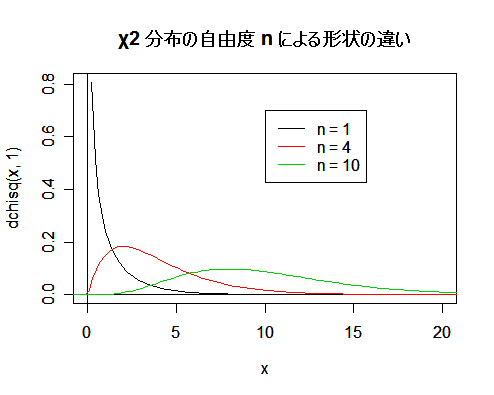
| curve(dchisq(x, 1), 0, 20) | # 自由度 1 の χ2 分布のグラフの表示 |
| abline(v=0, h=0) | # x 軸と y 軸の表示 |
| curve(dchisq(x, 4), add=T, col=2) | # 自由度 4 の χ2 分布のグラフを色 2(赤)で追加 |
| curve(dchisq(x, 10), add=T, col=3) | # 自由度 10 の χ2 分布のグラフを色 3(緑)で追加 |
| legend(10, 0.7, c("n = 1", "n = 4", "n = 10"), lty=1, col=c(1, 2, 3)) | |
| title(main="χ2 分布の自由度 n による形状の違い") | # タイトル |
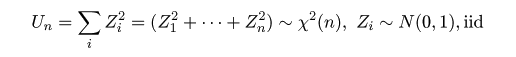
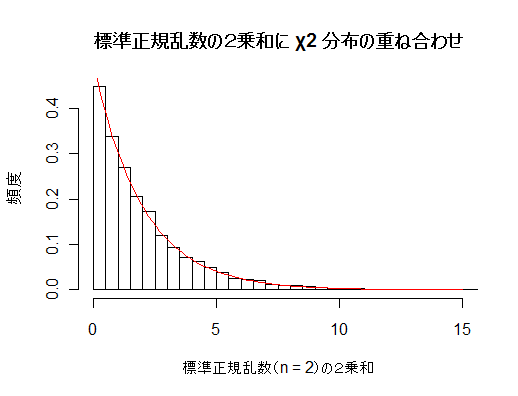
| N <- 10000 | # 乱数列の長さ |
| n <- 2 | # 自由度 |
| u <- matrix(rnorm(n*N), ncol=n) | # N×n の標準正規乱数乱数行列 |
| u2 <- u^2 | # 行列の要素の2乗 |
| un <- apply(u2, 1, sum) | # 行ごとの和 |
| umx <- ceiling(max(un)) | # 最大値を超える整数 |
| hist(un, breaks=seq(0,umx,by=0.5), freq=FALSE, xlim=c(0,15), xlab="Sum of squares of n normal random numbers", main="") | |
| curve(dchisq(x, n), 0, 15, add=T, col=2) | # 自由度 2 の χ2 分布の重ね合わせ |
| title(main="Histogram of sum of squares of \n normal random numbers") | # タイトル |
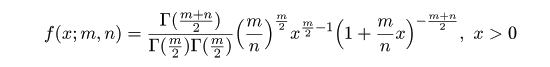
| op <- par(mfrow = c(1, 2)) | # |
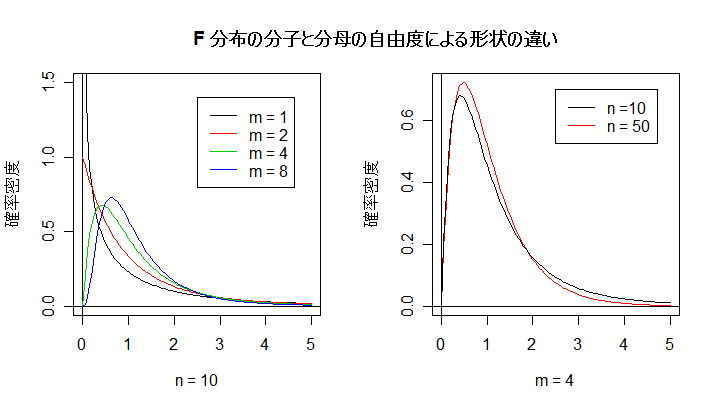
| curve(df(x, 1, 10), 0, 5, ylim=c(0,1.5), ylab="確率密度", xlab="n = 10") | # m = 1,n = 10 の F 分布 |
| abline(v=0, h=0) | # x 軸,y 軸 |
| curve(df(x, 2, 10), 0, 5, add=T, col=2) | # m = 2,n = 10 の F 分布 |
| curve(df(x, 4, 10), 0, 5, add=T, col=3) | # m = 4,n = 10 の F 分布 |
| curve(df(x, 8, 10), 0, 5, add=T, col=4) | # m = 8,n = 10 の F 分布 |
| legend(2.5, 1.4, c("m = 1", "m = 2", "m = 4", "m = 8"), lty=1, col=1:4) | # 凡例 |
| curve(df(x, 4, 50), 0, 5, col=2, ylab="確率密度", xlab="m = 4") | # m = 4,n = 50 の F 分布 |
| abline(v=0, h=0) | # x 軸,y 軸 |
| curve(df(x, 4, 10), 0, 5, add=T) | # m = 4,n = 10 の F 分布 |
| legend(2.5, 0.7, c("n =10", "n = 50"), lty=1, col=c("black","red")) | # 凡例 |
| par(op) | # |
| title(main="F 分布の分子と分母の自由度の違いによる形状") | # タイトル |
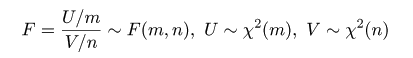
| N <- 10000 | # 乱数列の長さ |
| m <- 4 | # 分子自由度 |
| n <- 10 | # 分母自由度 |
| um0 <- matrix(rnorm(m*N), ncol=m) | # N×m の標準正規乱数乱数行列 |
| um2 <- um0^2 | # 行列の要素の2乗 |
| um <- apply(um2, 1, sum) | # 行ごとの和 |
| um <- um/m | # 自由度で割る |
| un0 <- matrix(rnorm(n*N), ncol=n) | # |
| un2 <- un0^2 | # |
| un <- apply(un2, 1, sum) | # |
| un <- un/n | # |
| fv <- um/un | # χ2 分布乱数の比 |
| fmx <- ceiling(max(fv)) | # fv の最大値を超える整数 |
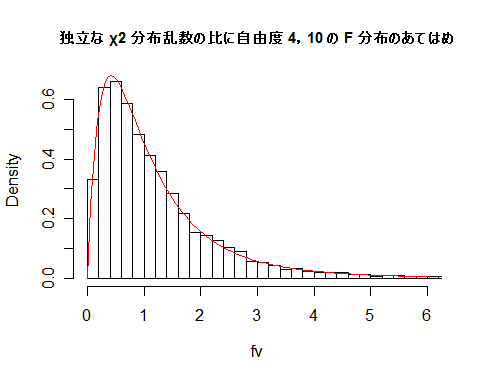
| hist(fv, breaks=seq(0,fmx,by=0.2), freq=FALSE, xlim=c(0,6), main="") | |
| curve(df(x, m, n), 0, 6, add=T, col=2) | # 自由度 4,10 の F 分布の重ね合わせ |
| title(main="Histgram of ratio of \n independent chi-squared random numbers") | |
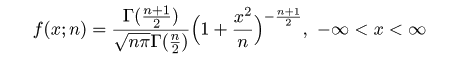
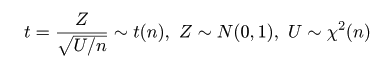
| N <- 10000 | # シミュレーション回数 |
| n <- 10 | # 1回のサンプルサイズ(自由度) |
| un0 <- matrix(rnorm(n*N), ncol=n) | # N×n の標準正規乱数行列 |
| un2 <- un0^2 | # 標準正規乱数行列の要素の2乗 |
| un <- apply(un2, 1, sum) | # 要素の2乗の各行の和(自由度 n の χ2 分布乱数 N 個) |
| unr <- sqrt(un/n) | # 自由度 n の χ2 分布乱数を n で割った平方根 |
| z <- rnorm(N) | # 標準正規乱数 N 個 |
| tv <- z/unr | # t 値 N 個 |
| tmx <- ceiling(max(abs(tv))) | # t 値 の絶対値の最大 |
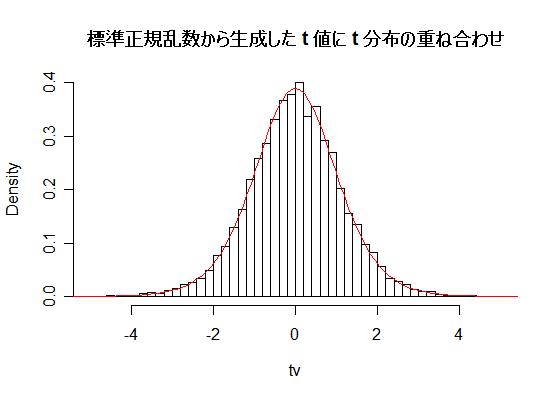
| hist(tv, breaks=seq(-tmx,tmx,by=0.2), freq=FALSE, xlim=c(-5,5), main="") | |
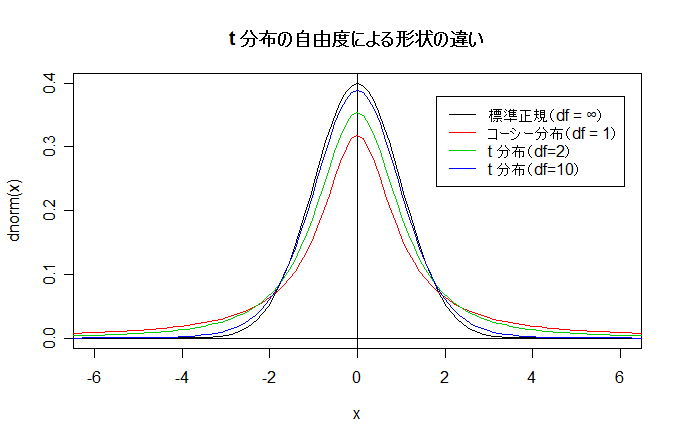
| curve(dt(x, n), add=T, col=2) | # 自由度 10 の t 分布の重ねがき |
| title(main="Histgram of t - values ") | |