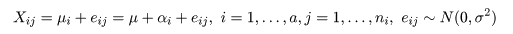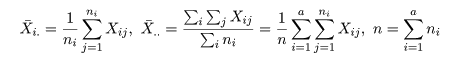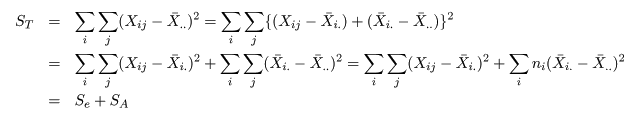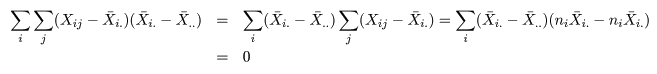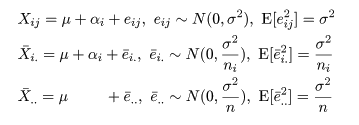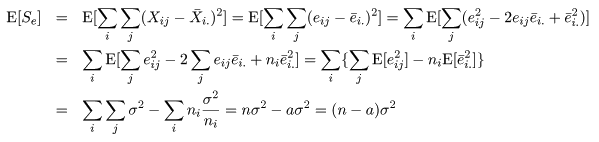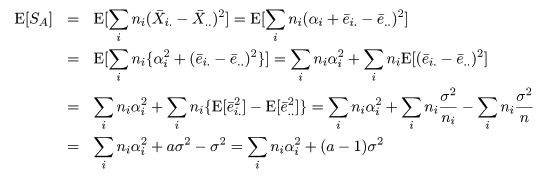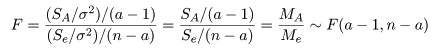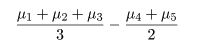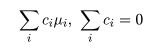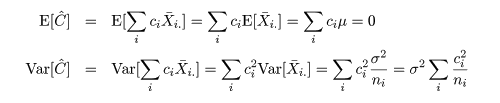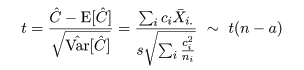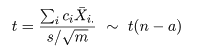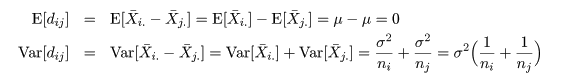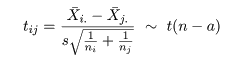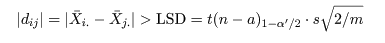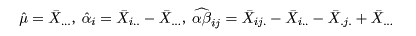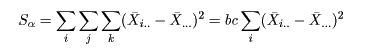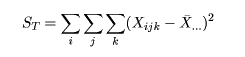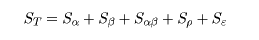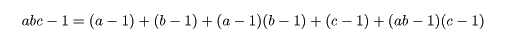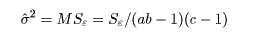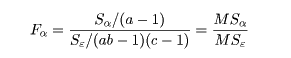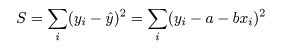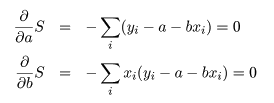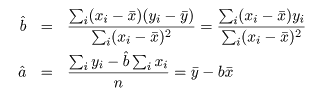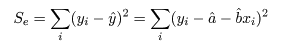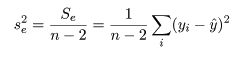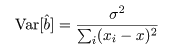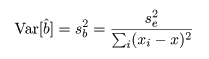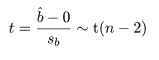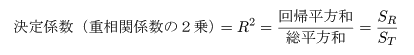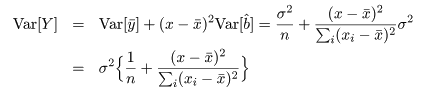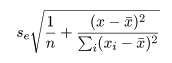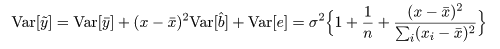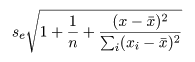東京農工大学
2020.10.30
生物統計学3
東京大学大学院農学生命科学研究科 大森宏
分散分析(Analysis of Variance)
分散分析は,ANOVA (Analysis of Variance) と略記されることもある.分散分析は,複数の処理を同時に
行ったときに,処理効果を推定するための最も基本的な手法である.データ全体の持つ情報は,総平方和
にまとめられているが,これを,処理の分散成分(処理平均平方)と誤差の分散成分(誤差平均平方)とに
分離して,その大きさを比較することにより,処理の効果を見積もるものである.
因子と水準
経済学では価格や成長率,工学では作業時間や故障率,農学では収量や抵抗性など,
調査研究したい特性を形質(character)という.着目した形質に影響を与えると考えられるもの,
例えば,収量では品種,温度,施肥量などを要因または因子(factor)という.
要因の影響を調べるためいくつかの品種を用いたり,
施肥量に段階を設けたりするが,それを水準(level)という.
一元配置(one-way layout)
構造モデル
t 検定では,2 つの処理平均の比較を行ったが,この節ではこれを拡張して,複数の処理平均の比較を行う
手法を考える.いま,a 水準の処理(treatment)A1,…,Aa,があり,
処理 Ai を行った ni 個の標本,
Xi1,…,Xini,が得られた
とする.処理 Ai からの標本は,平均 μi = μ + αi,分散 σ2
の正規分布に従うと仮定する.ここで,μ を総平均(grand mean),
αi を処理効果(treatment effect)もしくは,主効果(main effect)と言い,
Σiαi = 0,である.ここで,平均 0,分散 σ2 を持つ
誤差項(error term)eij を
導入し,標本の構造モデル,
として表現すると,データの持つ構造が理解しやすくなる.
平方和分解
いま,処理 Ai の標本平均を X-i.,
標本総平均を X-.. とすると,これらは,
と計算される.標本全体の持つ情報は,総平方和 ST(Total Sum of Squares)で表現される.これは,
のように誤差平方和 Se(Error Sum of Squares)と
処理平方和 SA(Treatment Sum of Squares)とに分解される.これは,積の項が
のように 0 となるからである.
なお,誤差平方和を群内平方和(within groups sum of squares),処理平方和を群間平方和(between groups sum
of squares)と呼ぶことも多い.
平方和の期待値
個々の標本 Xij と処理 Ai の標本平均 X-i.,
標本総平均 X-.. の構造モデルがそれぞれ,
のようになるので,誤差平方和 Se と処理平方和 SA の期待値は,それぞれ,
のように計算できる.
帰無仮説のもとでの平方和の比の分布
一元配置モデルにおける帰無仮説は,すべての処理効果がない,つまり,
H0:αi = 0,i = 1,…,a,
である.前節の平方和の期待値から,帰無仮説のもとで,Se/σ2 は自由度 n - a の
χ2 分布に従い,SA/σ2 は自由度 a - 1 の χ2 分布に
従うことがわかる.これらの χ2 分布をその自由度で割った比の F 値は,
のように自由度 a - 1,n - a の F 分布に従う.
ここで,MA は,処理平方和 SA を
その自由度 a - 1 で割ったもので,処理平均平方(treatment mean square)と呼ばれ,処理平均から求めた
誤差分散 σ2 の推定値である.一方,Me は,誤差平方和 Se を
その自由度 n - a で割ったもので,誤差平均平方(error mean square)と呼ばれ,誤差分散の推定値である.
帰無仮説のもとでは MA と Me はほぼ等しいことが期待されるので,その比 F 値は
1 に近いことが期待される.よって,F 値が大きな値をとるときは帰無仮説が正しくないと考え,帰無仮説を
棄却する.F 値が大きいか小さいかの判断基準が対応する自由度の F 分布で決められる.
分散分析表と F 検定
一元配置モデルの解析結果は,以下の分散分析表(ANOVA table)にまとめられる.
| 変動因 | 自由度(df) | 平方和(S.S.) |
平均平方(M.S.) | F 値 |
|---|
| 主効果 | a - 1 | SA |
MA = SA/(a - 1) | MA/Me |
|---|
| 誤 差 | n - a | Se |
Me = Se/(n - a) | |
|---|
| 全 体 | n - 1 | ST |
| |
|---|
この表から検定統計量 F 値が求められる.そして,
自由度 a - 1,n - a の F 分布の 1 - γ 点(例えば 95 %点)F(a - 1,n - a)1 - γ
より F 値が大きい,すなわち,
F > F(a - 1,n - a)1 - γ
であるとき,帰無仮説を棄却すると,有意水準 γ (例えば 5 %)の検定が行える.これを,F 検定(F test)
という.
対比(contarst)
処理平均 μi のある群と他の群との違いに特に興味がある場合がある.例えば,処理 1,2,3 の
平均と処理 4,5 の平均の間
に差があるかをみたいような場合である.一般に,
である比較を対比という.
対比 C = Σiciμi は C^
= ΣiciX-i. で推定されるが,
帰無仮説(αi = 0)のもとでは,
対比推定量の平均と分散は,
となるので,分散 σ2 をその推定量 s2 で置き換えた検定統計量 t は,
のように自由度 n - a の t 分布に従うので,対比 C = Σiciμi = 0 の
検定を行うことができる.特に,各処理水準の標本数が ni = m と一定で,対比の係数を
Σic2i = 1 と標準化すると,検定統計量は,
と簡略化される.
直交対比
ところで,別の対比 Σidiμi があったときに,
Σici di = 0,となるものを直交対比という.
直交対比の組は同時に検定ができる.
いま、処理 1,2,3, 4,5 の5つの処理があったとすると、処理 1,2,3 と処理 4,5 の平均との差を考えると、
この対比の係数ベクトルは、
c1 = (1/3, 1/3, 1/3, -1/2, -1/2)
となる。この対比に直交する対比係数ベクトルとしては、例えば、
c2 = (0, 0, 0, 1, -1)
c3 = (1, -1/2, -1/2, 0, 0)
などが考えられる。これらの対比係数ベクトルは互いに直交しているので、同時に検定ができる。
このように、事前に比較が決められるときは,後述する多重比較による有意確率の補正を行わない.
多重比較(multiple comparison)
分散分析(正確には実験計画)の文脈では,試験設計の段階で帰無仮説の設定が行われる.つまり,検定の内容
が事前に決定されている.このような「先付け」のときは,検定の数がそれほど多くないなら,
複数の検定を行っても有意水準についての補正を行わないのが普通だと思われる.
しかし,データが得られた後,「後付け」でどの処理間の差が有意であるか調べたい誘惑にかられることが多い.
結果として差が
大きかった処理間で t 検定を繰り返して行うと,たくさんの検定を行うので,たまたま有意になる確率が
名目上の有意水準(たとえば 5 %)を超えてしまう恐れがある.これが,多重比較である.現在では,
コンピュータにより多くの検定を簡単に行うことができるので,以前に比べて多重比較の問題を考慮しなければ
ならないと考えられる.
いま,処理平均 μi と μj の比較を行う場合を考える.
2 つの処理平均の差 μi - μj は,
dij = X-i. - X-j. で推定される.
帰無仮説(αi = αj = 0)のもとで,dij の平均と分散は,
となるので,分散 σ2 をその推定量 s2 で置き換えた
検定統計量 tij は,
のように自由度 n - a の t 分布に従うので dij = 0 の検定を行うことができる.
有意水準 α'(たとえば 5 %) の検定は,
自由度 n - a の t 分布の 1 - α'/2(たとえば 97.5 %) 分位点,
t(n - a)1 - α'/2 を用いて,
が成り立つとき μi と μj の効果に違いがあると判定される.ここで,
LSD(Least squared distance)は最小有意差という量で,以前は,α' = 0.05 として,処理効果のある組み合わせ
を見つけるためよく用いられていたが,最近は,多重比較を考慮に入れた有意水準の補正を考えるのが普通
なので,単純な LSD は使用しない方が良いと思われる.
いま,a 水準の主効果があったとすると,すべての組み合わせは r = a(a - 1)/2 通りあり,「後付け」の
検定を行うときは,全体で r 回の検定を行っていると考えなければならない.
R でも
対比較では多重比較による有意確率の補正が簡単に行える.
多重比較法の比較
多重比較の方法はここで取り上げた以外の手法も知られているが,R で手軽に使える手法を解説した.
ここで紹介した手法の有意水準をシミュレーションで比較してみる.標準正規乱数 50 を 1 から 5 まで
のグループに 10 個ずつ分ける.このデータを処理数 a = 5,処理内標本 n = 10 の一元配置データ
とみなす.このデータは帰無仮説が真のときで,処理平均に差がないはずである.
シミュレーションデータに対する分散分析と対比、多重比較
# start of script
a <- 5; n <- 10 # 処理水準数 a,処理内標本数 n
x <- rep(1:a, each=n)
x <- factor(x) # ラベル化
y <- rnorm(n*a) # 標準正規乱数
cbind(y, x) #
boxplot(y ~ x)
av <- aov(y ~ x) # 分散分析
summary(av)
av2 <- lm(y ~ x) # 線形モデル
anova(av2) # 分散分析
# 対比
c1 <- c(1/3,1/3,1/3,-1/2,-1/2) # 対比係数ベクトル
c2 <- c(0, 0, 0, 1, -1)
c3 <- c(1, -1/2, -1/2, 0, 0)
contrasts(x) <- cbind(c1, c2, c3) # 対比の定義
contrasts(x) # 定義した残りの直交対比は R が勝手につくる
fc <- lm(y ~ x) # 対比つき線形モデル
summary(fc) # 結果表示(最初の3つの対比のみに着目)
# 多重比較
pt <- pairwise.t.test(y, x); pt # 対比較ホルム補正
which(pt$p.value < 0.05, arr.ind=T)
pt <- pairwise.t.test(y, x, p.adj = "bonf"); pt # 対比較ボンフェローニ補正
which(pt$p.value < 0.05, arr.ind=T)
pt <- pairwise.t.test(y, x, p.adj = "none"); pt # 対比較補正なし
which(pt$p.value < 0.05, arr.ind=T)
th <- TukeyHSD(av); th # チューキー HSD
which(th$x[,4] < 0.05)
# end of script
|
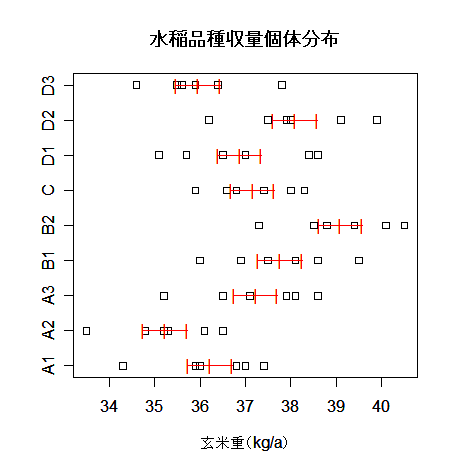
品種によるコメの収量の違い
水稲の9品種をそれぞれ,6区画の水田で栽培したときのアール当たりの玄米重量は以下のようであった.
このうち,A,B,D,それぞれ,同じ母本から育成された品種であり,C は標準(対照 control)品種である.
このデータは一元配置分散分析で解析できる.処理が品種で,9 水準からなっている.帰無仮説は,
H0:収量はどの品種も同じである
である.
データダウンロード
データの品種ごとのちらばりと,品種平均と標準誤差を視覚化する
yy <- read.csv("hinsyu.csv"); yy # csv データ読み込み
n <- nrow(yy)
a <- ncol(yy)
nn <- n*a # 総データ数
xm <- 1:a
ym <- mean(yy) # 品種ごとの平均
se <- sum(diag(var(yy)*(n-1))) # 誤差平方和
ve <- se/(nn - a); ve # 誤差平均平方(誤差分散)
vm <- ve/n # 品種平均の分散
svm <- sqrt(vm) # 品種平均の標準誤差
stripchart(yy, xlab="Yield (kg/a)") # 品種ごとの個体分布表示
text(ym, xm,"|", col="red") # 品種平均
text(ym+svm, xm,"|", col="red") # 品種平均 + 標準誤差
text(ym-svm, xm,"|", col="red") # 品種平均 - 標準誤差
segments(ym-svm, xm, ym+svm, xm, col="red")
|
-
多元配置
実験計画法
因子と水準
作物において,収量や抵抗性などの調査研究したい特性を形質(character)という.
着目した形質に影響を与えると考えられる品種,温度,施肥量などを
要因または因子(factor)という.要因の影響を調べるためいくつかの品種を用いたり,
施肥量に段階を設けたりするが,それを水準(level)という.
要因と水準を決定したら,その反応を調べるためには,圃場で実際に栽培してみる
必要がある場合が多い.
しかしながら,圃場の環境条件は場所により異なり,均一の条件で栽培管理を行うことは
難しい.環境条件に多少のばらつきがあると想定される場合には,ばらつきの影響を無作為化
する必要がある.これを行うのが,実験計画法である.
Fisher の3原則
実験計画の創始者である R.A. Fisher が提唱した原則で,
反復(replication),無作為化(randomization),局所管理(local control)
の3つからなる.これらは,
処理の違いに基づく差が偶然の誤差を超えて有意なものかどうか統計的に判定するため,
実験を行うにあたり必要な管理原則である.この原則に基づいて圃場での実験配置が設計される.
反復
1つの処理組み合わせに対して,少なくとも2回以上の繰り返しが必要である.
繰り返しにより,誤差の大きさが評価できる.
無作為化
実験順序や,空間配置の無作為化.ある特定の処理条件を圃場のある特定の場所にかためて
しまうと,その場所がたまたま水はけがよかったり肥沃だったりした場合,処理効果によるものか
場所の効果によるものかの判別ができなくなる.
このようなある特定の場所による効果を系統誤差(systematic error)というが,
無作為に処理条件を配置させることにより,系統誤差を偶然誤差(random error)に転化させる
ことができる.
局所管理
実験が大規模で,実験全体を無作為化したら誤差が大きくなってしまうような場合,
実験をある程度細分化してブロックを構成し,ブロック内で処理条件を無作為化する.
ブロック内のバックグラウンドはなるべく均一になるように管理できれば,
系統誤差の一部がブロック間変動として除去できるので,実験誤差が
小さくなる.
よく用いられる試験配置
1996年度から2000年度(1998年度を除く)までの試験目的は,品種,肥料水準,栽植密度が
水稲の収量構成要素に与える影響を計測するためであった.その配置は2反復2要因乱塊法であった.
2000年度試験配置
データダウンロード
収量とは,単位面積(m2)あたりの玄米の収穫量(g), (grain yield; gy)のことであるが,収量構成要素は,
収量に影響を与える形質で収量を分解したもので,たとえば,「単位面積あたりの穂数(panicle number; pn)」,
「一穂籾数(grain number; gn)」,「登熟歩合(percentage of riped grains; pr)」,
「玄米千粒重(g),(1000-grain weight; gw)」と分解できる.収量はこれらの構成要素の積で表現される.
今回の実験では「日本晴」データの解析を行う.
特定年次の解析
構造モデル
ある年次における処理組み合わせでラベルをつけた収量値 Xijk は,処理効果により,
Xijk = μ + αi + βj + ρk
+ (αβ)ij + εijk, i = 1,2, j = 1,2,3, k = 1,2
と構造化(モデル化)できる.ここで,μ は総平均で
αi は栽植密度の
主効果(main effect)であり,βj は施肥量主効果,
ρk はブロック効果,(αβ)ij は栽植密度と施肥量の交互作用(interaction)で,
各効果の和は0,たとえば,Σ αi = 0,とする.
また,εijk はこれらの効果で説明できない誤差で,
互いに独立に
平均 0,分散 σ2 の正規分布(normal distribution)
に従う (εijk ~ N(0, σ2)) と仮定する.
各効果の推定値は,たとえば,
と表せる.
処理平方和
効果の大きい処理に対しては各効果の水準ごとの推定値は大きく異なり,逆に各水準
ごとに同じような値の推定値を与えるような処理は効果が小さいと考えられる.
これは処理平方和(sum of squares; SS)で測ることができる.
たとえば,密度の主効果の平方和は,
である.実は,
データがもつ全平方和(sum of squares; SS)
は,以下に示すように各処理による平方和で分解され,
となる.これと同様に,各処理平方和に対する自由度(degree of freedom)も
となる.なお自由度とは,比較の数のことで,3 水準の試験では比較は 2 通り
(水準 1 対水準 2,水準 2 対水準 3)なので自由度は 2 となる.
また,比較 1 つ分の平方和が平均平方(mean squares; MS)で,
平方和を自由度で割った値である.たとえば,密度効果の平均平方は,
MSα = Sα/(a - 1) である.
また,誤差分散は,
のように誤差平均平方で推定する.各効果の大きさは,この
誤差の大きさと比較することにより測ることができる.
F 検定
各処理にまったく効果がないという帰無仮(null hypothesis),つまり,
H0 : αi = 0, βj = 0
という条件のもとで各処理効果の平均平方を誤差平均平方で割った値が F 分布に従う
ことにより各処理効果の検定(test)が行える.たとえば,密度主効果の検定は,
を用いる.密度効果がなければ Fα は 1 に近い値をとる.大きな
値を取った場合は,密度効果がないという帰無仮説が成立しておらず,
密度効果が認められると考える.つまり,帰無仮説を棄却(reject)する.
この大きさの基準として,慣習的に F 分布(自由度 a - 1, (ab - 1)(c - 1) )の
5 % や 1 % 点が用いられている.この基準確率を
有意水準(significance level)という.
収量に対する処理効果の分散分析表
| 要因 | 自由度 | 平方和 | 平均平方 |
F 値 | p 値 |
| ブロック | 1 | 15862 |
15862 | 3.85 | 0.107 |
| 密度 | 1 | 1419 |
1419 | 0.348 | 0.583 |
| 施肥 | 2 | 65029 |
32514 | 7.898 | 0.028 | * |
| 密度×施肥 | 2 | 2222 |
1111 | 0.270 | 0.774 |
| 誤差 | 5 | 20583 |
4117 | | |
|
| * : 5 % 有意 |
分散分析表の見方
各処理の効果の程度を
まとめたのが分散分析(analysis of variance; ANOVA)
であり,その結果は上の表にまとめられている.
これをみると,施肥量の効果の平方和は3水準で Sβ=65029 となり,比較は2通り
なので自由度は2となる.その平均平方は平方和を2で割り,MSβ=32514 である.
この値と誤差平方和の比が F 値で,7.90と大きな値になった.
帰無仮説のもとで F 値より大きな値がでる確率が p 値(p - value)である.p 値が小さいことは,
帰無仮説が成立する可能性が小さい,つまり,
処理効果が存在する可能性が大きいことを意味する.
この例では,統計的にみて
有意水準 3 % で施肥量により収量が異なるといえるが,他の処理
効果は認められなかったという結論になる.つまり,平均値から得た類推は,
統計的に根拠があったということになる.
複数年次にわたる解析
構造モデル
4年間にわたって行った
データ表
を用いると,
気象条件などの年ごとの違いによる効果がわかる.
年次効果を γk で表すとすると,
Xijkl = μ + αi + βj + γk
+ (αβ)ij + (βγ)jk + (αγ)ik
+ (αρ)il + εijkl
という 3 元配置モデルで記述できる.なお、3次交互作用は解釈が難しいので取り出さなかった。また,ブロック効果
は、毎年管理者や圃場が変わるので年次とブロックの交互作用で取り出した。
分散分析表をみると,年次効果と施肥量効果は主効果と交互作用ともに有意
となったが,密度に関しては有意とはならなかった.どのような効果が存在するかをみるため,
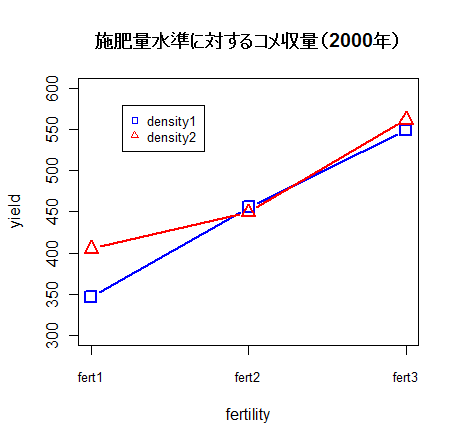
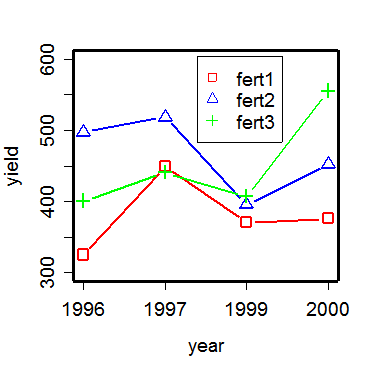
年次と施肥量水準の 組み合わせごとの平均を図にプロットした.
これをみると, 年次ごとに収量に変動があることがわかる.また, 無肥料区(fert1)と少肥料区(fert2)は
年次ごとの変動が似ていて,少肥料区の方が収量が高くなっているが,
多肥料区(fert3)は2000年のように高収量のときもあるが,1996年や1997年のようにそれほど高い収量が得られない場合
もあり,これが交互作用として検出されている.
これは,多肥料区で繁茂しすぎて 倒伏が起こった年があったためと考えられる.
収量に対する年次効果と処理効果の分散分析表
| 要因 |
自由度 |
平方和 |
平均平方 |
F 値 |
p 値 |
| 密度 |
1 |
125 |
125 |
0.033 |
0.8563 |
| 施肥 |
2 |
67405 |
33703 |
9.056 |
0.0010 |
** |
| 年次 |
3 |
54399 |
18133 |
4.872 |
0.0081 |
** |
| 密度×施肥 |
2 |
2352 |
1176 |
0.316 |
0.7319 |
| 施肥×年次 |
6 |
75051 |
12508 |
3.361 |
0.0138 |
* |
| 密度×年次 |
3 |
2376 |
792 |
0.213 |
0.8866 |
| 年次×ブロック |
4 |
21144 |
5286 |
1.420 |
0.2552 |
| 誤差 |
26 |
96762 |
3722 |
|
|
| * : 5 % 有意,**:1 % 有意 |
「日本晴」収量の年次効果と施肥水準によるプロット(1996 ~
2000年度)
|
- コメ収量複数年次の分散分析
yield <- rice$gy # gy 列を取り出す
dens <- factor(rice$density) #密度水準ラベル化
fert <- factor(rice$fert)
year <- factor(rice$year)
blk <- factor(rice$rep)
rya.aov <- aov(yield ~ dens + fert + year + dens:fert + fert:year
+ dens:year + year:blk)
summary(rya.aov)
#
#「日本晴」収量の年次効果と施肥水準によるプロット
x <- tapply(rice$gy, fert:year, mean)
plot(1:4, x[1:4], type="b", lwd=2, cex=1.5, xaxt="n", xlab="year", ylab="yield",
ylim=c(300,600), pch=0, lty=1,cex.lab=1.2, cex.axis=1.2, col="red")
axis(1, 1:4, labels=levels(year), cex.axis=1.2)
box(lwd=3)
points(1:4, x[5:8], type="b", pch=2, lwd=2, lty=1, col="blue", cex=1.5)
points(1:4, x[9:12], type="b", pch=3, lwd=2, lty=1, col="green", cex=1.5)
legend(2, 600, legend=c("fert1","fert2","fert3"), pch=c(0,2,3),
col=c("red","blue","green"), cex=1.2)
title(main="Yield of 'Nipponbare' to year effects and fertility levels")
|
回帰分析(Regression Analysis)
直線回帰
モデル
2つの変数 x ,y に対し,y の値が x の値の動きにつれて
線形的に変化すると仮定される,つまり,
y = a + b x
という関係が成り立っていると考えられる場合である.これを y の x に
対する直線回帰といい,a ,b を回帰係数という.
また,変数 y を従属変数,目的変数といい,変数 x を独立変数,説明変数と
いう.
最小2乗法
データに最もよくあてはまる直線回帰式を得るには,データ点
(xi ,yi ),
と回帰による推定点,
(xi ,y^i ),
y^i = a + b xi ,
の間の距離の2乗和 S が最小になるような回帰係数 a ,b を求める.つまり,
を最小化する a ,b を求める問題に帰着する.これを最小2乗法という.
これは,S を a ,b で偏微分して 0 とおくことによって得られる.つまり,
の連立方程式を a ,b で解けばよい.これより,回帰係数の推定値 a^,
b^ が,
と得られる.
回帰式の統計モデル
推定された直線回帰式がどの程度現実のデータに適合しているかを調べるために,
回帰式が従う統計モデルを考える.標本の格データ点,
(xi ,yi ),
が,
yi = a +
b xi +
ei ,
ei
~ N( 0,σ2 )
であると仮定する.ei は誤差(error),あるいは,
残差(residual)で,直線回帰
式では説明がつかない部分を表し,これが互いに独立に平均 0,分散 σ2
の正規分布に従うと仮定する.誤差の大きさが大きいときは,直線回帰式ではデータが説明できない
と考える.
残差分散と回帰係数の標準誤差
回帰で説明がつかない残差平方和 Se は,
で求められる.これの自由度は n-2 であるので(2つの回帰係数分の自由度を除く),回帰の
残差(誤差)分散の推定値は,
で求められる.
一般に,Var(yi )
= σ2 であるとき,その定数(c)
倍の分散は,
Var(cyi ) = c2σ2,
Var(Σici
yi ) =
Σici
2 σ2
であり,従属変数 y のデータ yi は,
yi
~ N( a + b xi ,σ2 )
と分布するので,回帰係数の推定値 b^ の分散は,
となる.この分散の平方根を回帰係数推定値 b^ の標準誤差という.
回帰係数の標準誤差による t 検定
目的変数 y が説明変数 x との回帰関係にないという
帰無仮説,
H0:b = 0,
を考えてみよう.
回帰係数 b の推定値 b^ の分散は,
と推定できるので,b^ の標準偏差(標準誤差)は, s b と推定
される.これより,回帰係数をその標準誤差で割った t 値が,帰無仮説のもとで,
のように,自由度 n-2 の t 分布に従うことを利用して回帰係数の検定が行える.すなわち,
自由度 n-2 の t 分布の 97.5%点を t0 とすると,
|t | > t0 → 帰無仮
説を有意水準 5 %で棄却(回帰関係が有意に認められる)
|t | ≦ t0
→ 帰無仮説を棄却しない(回帰関係が認められない)
と定式化できる.
分散分析
平方和分解
回帰式により,
従属変数 y のデータ yi は,
yi = y^i
+ (y^i -
yi ) =
回帰値 + 残差
のように分解される.この分解に対応して従属変数データの総平方和 ST は,
ST = Σi
(y i - y- )
2 =
Σi
(y^i - y- )
2 +
Σi
(y i -
y^i )
2 = SR + Se
総平方和 = 回帰平方和 + 残差平方和
のように分解される.これを平方和の分解という.この分解に対応して自由度は,
n-1 = 1 + n-2
と分解される.
決定係数(重相関係数の2乗)
データが直線回帰式でよく説明できるのは,回帰平方和が大きく,残差平方和
が小さい場合である.総平方和のうち回帰平方和で説明される割合を決定係数,もしくは
重相関係数の2乗といい,
で定義される.なお,重相関係数 R とは,データ y i
と回帰値 y^i との間の相関係数である.これより,
以下の分散分析表ができる.
回帰分析の分散分析表
| 変動因 | 平方和 | 自由度 | 平均平方 | F 値 |
| 回帰 | SR | 1 |
SR |
F = SR/se2 |
| 残差 | Se | n-2 |
se2 = Se/n-2 |
|
| 全体 | ST | n-1 |
|
|
F 検定
従属変数 y が説明変数 x の回帰関係にないという
帰無仮説,
H0:b = 0,
を考える.帰無仮説のもとでは,回帰平均平方 SR と残差分散 se2
がともに誤差 σ2 の不偏推定量になるので,
その比 F 値が,
F = SR/se2
~ F(1,n-2),
という F 分布に従うことを利用して検定ができる.すなわち,分子,分母
自由度が 1,n-2 である F 分布 F(1,n-2) の95%点を F0 とすると,
F > F0 → 帰無仮説を有意水準 5 %で棄却(回帰関係が有意に認められる)
F ≦ F0 → 帰無仮説を棄却しない(回帰関係が認められない)
と定式化できる.
回帰係数に対する検定
前節では,H0:b = 0,の検定を考えたが,もっと一般の形の検定,
H0:b = b0,
も簡単に考えることができる.このときは,帰無仮説のもとで,
t = (b^ - b0)/s b ~ t(n-2)
のように,自由度 n-2 の t 分布に従うことを利用して回帰係数の検定が行える.すなわち,
検定統計量として,この |t| 値を考えればよい.
回帰式の信頼区間
回帰係数の信頼区間
回帰係数の標準誤差 s b を用いて,
回帰係数 b の信頼区間がつくれる.すなわち,
自由度 n-2 の t 分布の 97.5%点を t0 とすると,
回帰係数 b の 95%信頼区間の幅 d は,d = t0
s b となるので, 95%信頼区間は,
b^ - t0
s b < b <
b^ + t0
s b
となる.
回帰直線の信頼区間
データから推定された回帰直線は,データの平均(x-,y-)
を通るので,
Y = y- + b^
(x - x-)
とおける.これより,Y の分散は,
となる.誤差分散 σ2 は,
データの残差分散 se2 で推定されるので,Y の標準誤差は,
となり,これが自由度 n - 2 を持つ.よって,推定回帰式にこの標準誤差の t0
倍を加えたものが,回帰式の 95%信頼幅となる.
回帰予測値の信頼幅
回帰式から得られる予測値 y~ は,回帰式に誤差項が加わって,
y~ = y- + b^
(x - x-)+ e
となるので,その分散は,
となる.先ほどと同様に,誤差標準偏差を残差標準偏差で置き換えると,回帰予測値 y~ の
標準誤差は,
となり,回帰式の 95%信頼幅の外側に回帰予測値の 95%信頼幅が描ける.
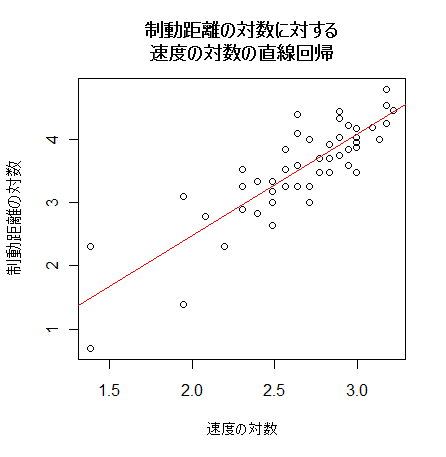
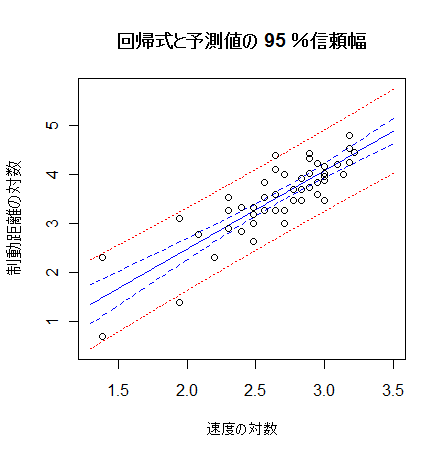
- 自動車の速度と制動距離の回帰係数に対する検定
物理法則によると,自動車の速度の2乗と制動距離が比例するので,求めた回帰係数は 2 となることが
期待される.このため,H0:b = 2,の検定を行ってみる.
これは,回帰係数の信頼区間を求め,これが 2 を含むかどうかでも調べることもできる.
bh <- summary(car.lm)$coefficient[2,1] # 回帰係数
sb <- summary(car.lm)$coefficient[2,2] # 回帰係数の標準誤差
tv <- abs(bh - 2)/sb; tv
edf <- summary(car.lm)$df[2] # 残差分散の自由度
1 - pt(tv, df=edf) # 有意確率
t0 <- qt(0.975, df=edf)
d <- t0*sb
bh - d # 95%信頼区間の下限
bh + d # 95%信頼区間の上限
new <- data.frame(x=seq(1.3, 3.5, by=0.02))
dc <- predict(car.lm, new, interval="confidence", level=0.95) # 回帰推定値(回帰直線)の 95 %信頼幅
dp <- predict(car.lm, new, interval="prediction", level=0.95) # 回帰予測値の 95 %信頼幅
matplot(new$x, cbind(dc,dp[,-1]), lty=c(1,2,2,3,3), type="l",
col=c("blue","blue","blue","red","red"), xlab="log of velocity", ylab="log of braking distance")
points(x, y)
|
ミヤマクワガタの相対成長解析
データダウンロード
成長段階の異なる 47 頭のミヤマクワガタのパーツ別の重量データ(g).パーツは,
頭部(WHEAD),前胸部(WTHORAX),中胸~腹部(WABDOM),交尾器(WGENI)からなる.
形態形質 x,y に対して,初期成長指数を a,成長比を b と
したときの生物形態の相対成長式,
logy = loga + b logx
において,中胸~腹部(WABDOM)の重量(g)を体サイズの指標 x としたとき,y として
頭部(WHEAD)の重量(g),前胸部(WTHORAX)の重量(g),交尾器(WGENI)の重量(g)
の3通りを考えたときの相対成長式の回帰係数をそれぞれ求める.
体の成長に合わせてパーツも比例して大きくなれば,成長比 b = 1 となるはずである.
参考文献(古い順)
- Introduction to the Theory of Statistics, Mood, A. M., Graubill, F. A. & Boes, D. C., 1974,
McGRAW-HILL
- 「実験」生産環境生物学,東京大学大学院農学生命科学研究科生産・環境生物学専攻編,1999,朝倉書店
- 工学のためのデータサイエンス入門-フリーな統計環境Rを用いたデータ解析-,間瀬茂ら,2004,
数理工学社
- 実践生物統計学-分子から生態まで-(第 1 章,第 2 章),
東京大学生物測定学研究室編(大森宏ら),
2004,朝倉書店
- The R Tips データ解析環境 R の基本技・グラフィックス活用集,船尾暢男,2005,九天社
- R で学ぶデータマインニング I -データ解析の視点から-,熊谷悦生・船尾暢男,2007,九天社
- R で学ぶデータマインニング II -シミュレーションの視点から-,熊谷悦生・船尾暢男,2007,九天社
Copyright (C) 2008, Hiroshi Omori. 最終更新日:2019年11月28日