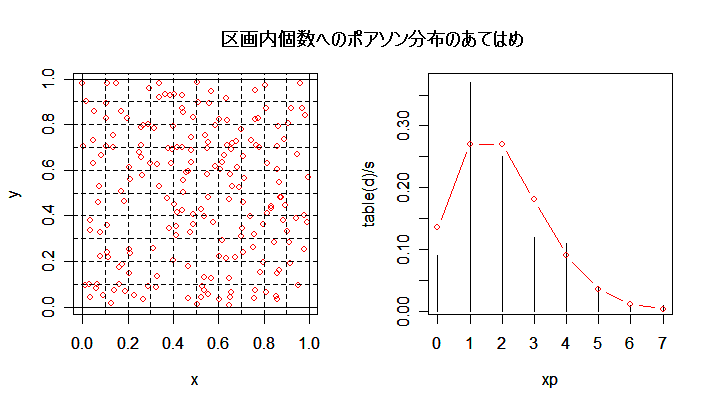
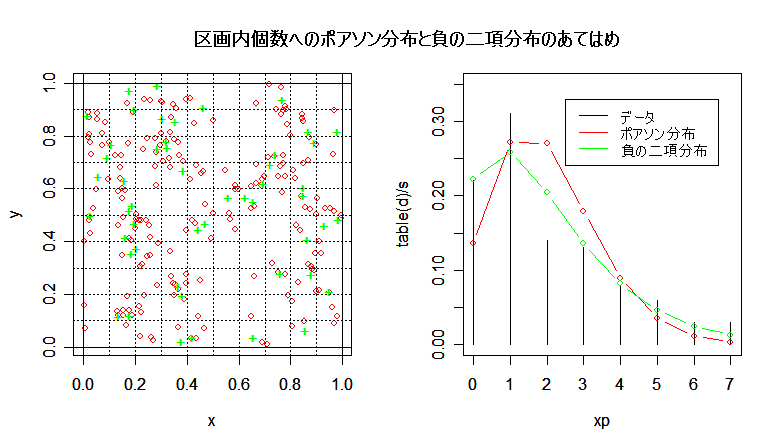
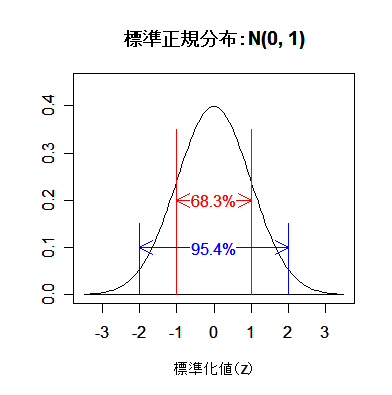
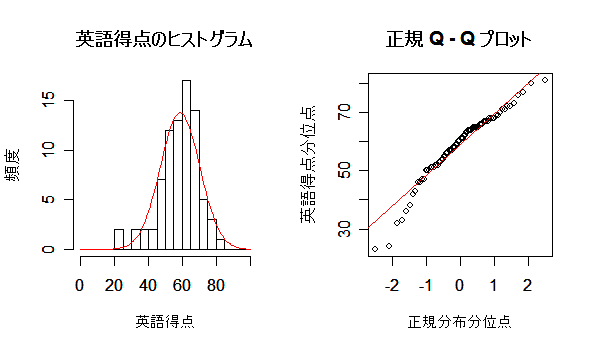
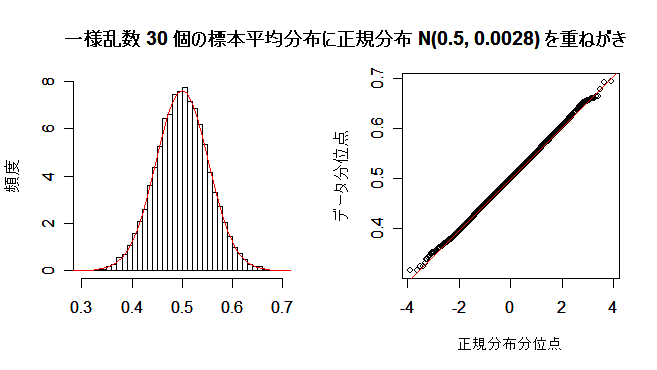
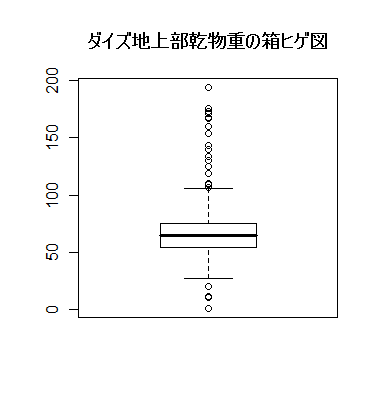
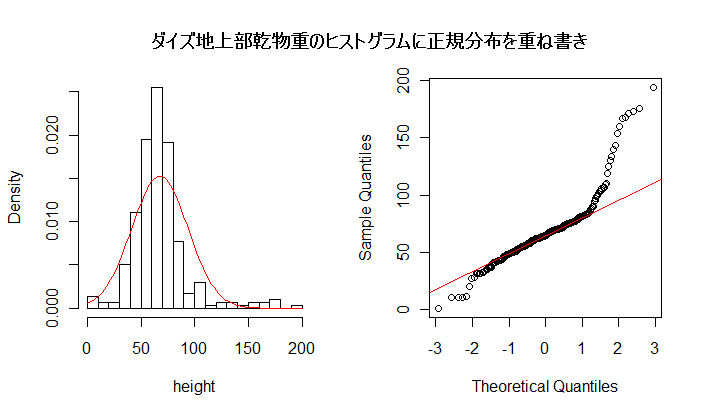
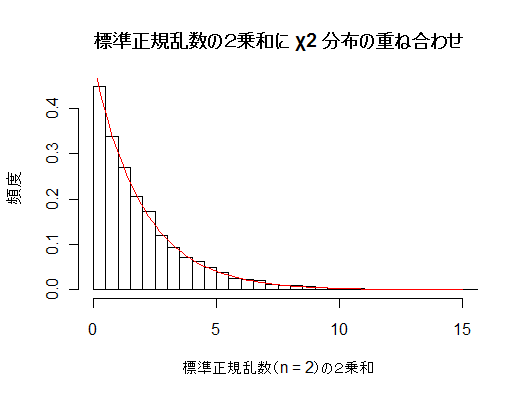
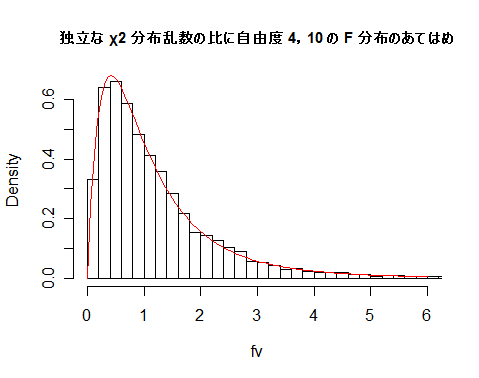
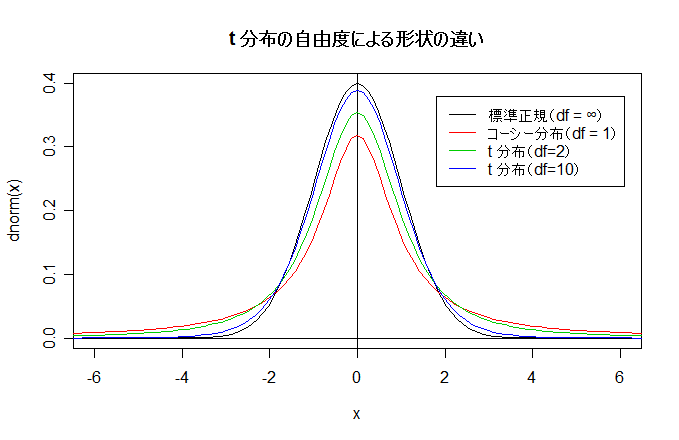
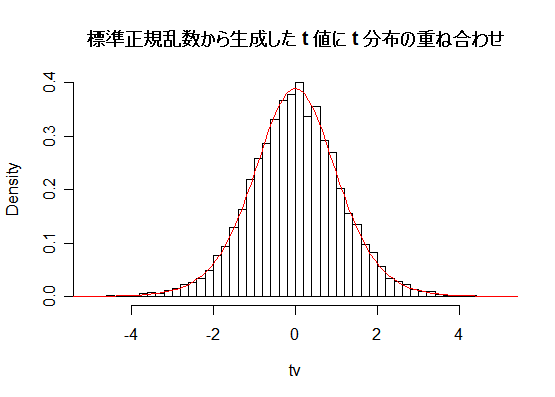
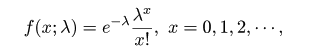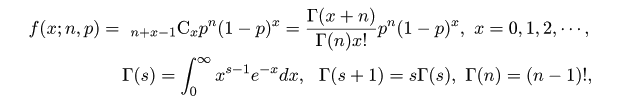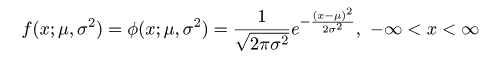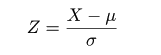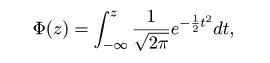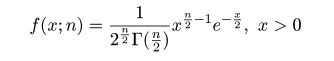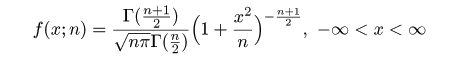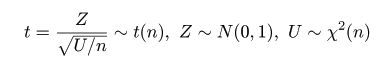# #以下はコメント文なので,R には読み込まれず,無視される. # # 英語得点データを用いて,データの基本統計量の計算演習を行う. # #英語の得点 eigo <- c( # 36,70,56,68,76,60,50,63,62,42,64,60,50,68,71,67, 50,65,67,57,72,64,61,66,46,80,46,51,59,32,55,65, 65,52,57,64,23,57,53,54,38,71,57,69,77,61,51,64, 63,43,65,61,51,69,72,68,53,66,68,58,73,65,62,67, 47,81,47,52,59,33,56,66,67,52,58,65,24,58,54,55) length(eigo) #データ数 mean(eigo) #標本平均 var(eigo) #標本分散 sd(eigo) #標本標準偏差 boxplot(eigo, main="英語得点の箱ヒゲ図") #箱ひげ図 boxplot.stats(eigo) #箱ひげ図用統計量 summary(eigo) #英語得点データの要約 hist(eigo, breaks=seq(0, 100, by=5), xlab="English score", ylab="Frequency", main="") title(main = "英語得点のヒストグラム") #グラフタイトル stem(eigo, scale=2) #幹葉表示 # # 散布図と回帰直線 # x <- 1:10 #連続した自然数 y <- c(3,5,6,6,9,10,6,9,10,7) plot(x, y) # データの散布図 reg <- lm(y ~ x) # 回帰の計算 summary(reg) # 回帰の結果表示 reg$coefficients # 回帰係数 abline(reg, col="red") # 回帰直線の表示 cor(x, y) # 相関係数
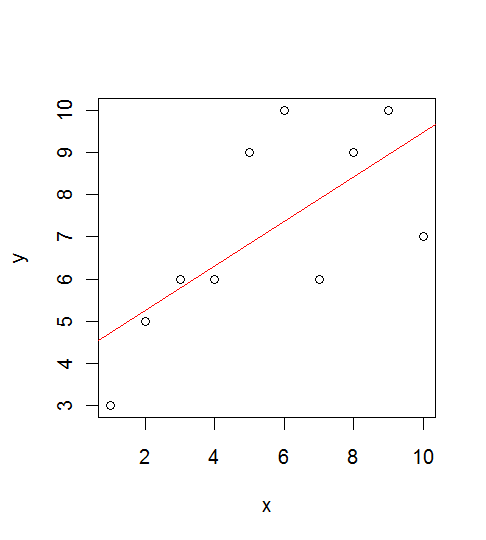
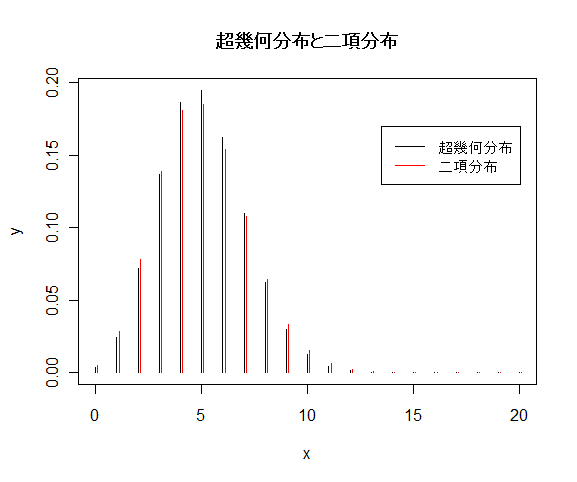
回帰直線:y = 4.2 + 0.527x
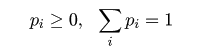
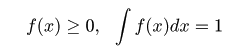
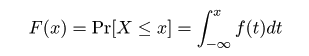
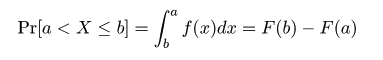
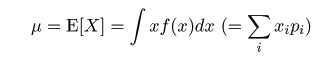
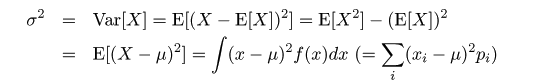
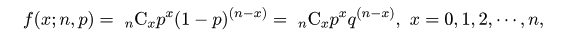
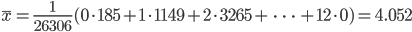 ,
,
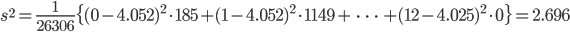
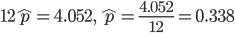
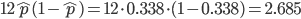


![{\rm E}[X]=kp](images2/EXTERN_0016.png) ,分散:
,分散:![{\rm Var}[X]=kp(1-p)(m+n-k), \ p=\frac{m}{m+n}](images2/EXTERN_0017.png)