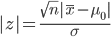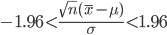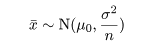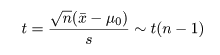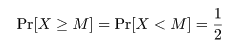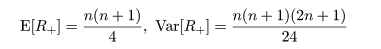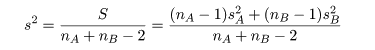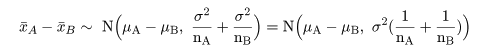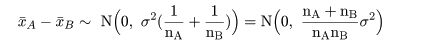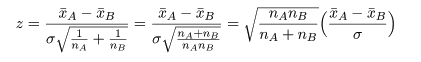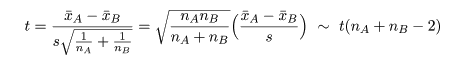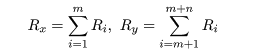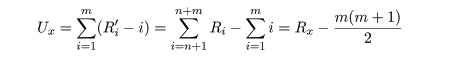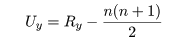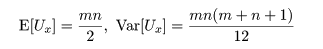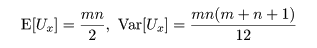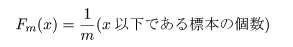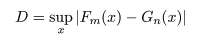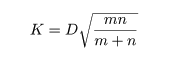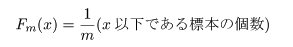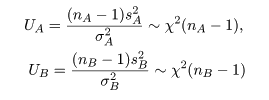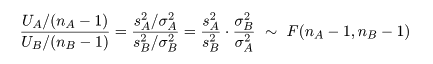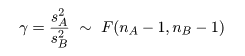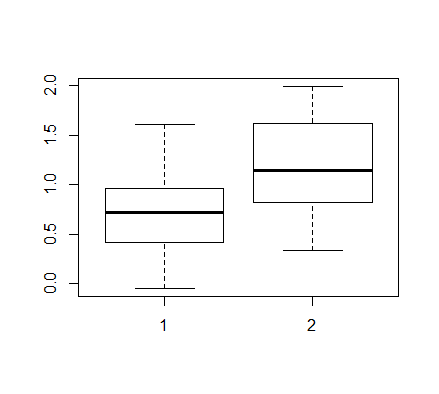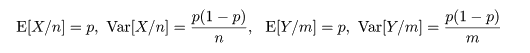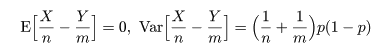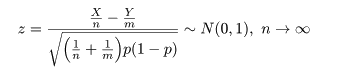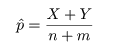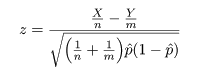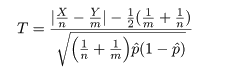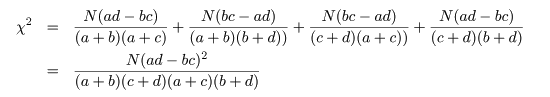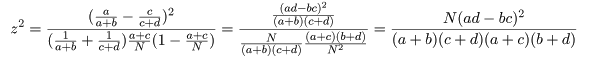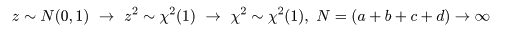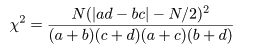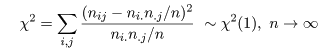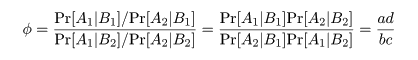2015年度生物測定基礎実験
2015.9.24
統計解析2
東京大学大学院農学生命科学研究科 大森宏
この実験の目的
統計解析ソフトRを用いて,統計解析の理論と実践を学ぶ.
正規母集団からの標本に基づく推論
独立な正規分布の合成分布
平均 μ1,
分散 σ12,の正規分布
からの標本 X ~
N( μ1,σ12 )
と,
平均 μ2,
分散 σ22,の正規分布
からの標本 Y ~
N( μ2,σ22 )
があり,両者が互いに独立であるとする.(Y の値は X の値の影響を受けない.)
正規分布に基づく母数の区間推定
正規分布は,平均 μ と分散 σ2 の2つの母数を持つ.
2つの母数とも未知であるのが普通であるが,片方が既知であるときは母数に関する推論は
簡単に行える.このため,多少非現実的な設定であるが,まず,既知の場合を考え,その後,より
一般的である2つの母数とも未知である場合を扱う.
分散既知の場合の母平均 μ の区間推定
正規分布する母集団で母分散 σ2
がわかっている場合は,未知の母平均 μ に関する区間推定は以下のように行える.
いま,正規分布 N( μ,σ2 ) において,大きさ n の標本
x1,x2,…,xn
を抽出したとき,母平均は標本平均で推定される.標本平均 x- の分布は,
となる.標準正規分布の 97.5%分位点を z0.975(= 1.96)とすると,
標準正規分布する確率変数 z が -z0.975 から z0.975 に入る
確率は 0.95 となる.つまり,
となる.最後の式を母集団平均 μ の 95% 信頼区間(confidence interval)と言う.
このように,母数の信頼区間を標本から推定することを区間推定という.区間推定においては,
信頼区間の幅 2d が小さい程よい.すなわち,母分散が小さい母集団で,
標本の大きさ(サンプルサイズ)が大きい程,精度の高い推定が行える.
- 95% の意味
同じ正規母集団から標本抽出を繰り返すと,毎回標本平均として異なる値がえられ,それに
対応して信頼区間も異なる.この信頼区間の 95% が真の平均 μ を含む,という意味である.
つまり,100回の標本抽出により,100 個の信頼区間を作ったら平均的にみて,95 個の信頼区間が
真の平均 μ を含むことが期待できる.
下の図は,平均 0 分散 2 の正規分布 N( 0, 2 ) から大きさ 10 の標本を取りだし,分散が既知であるとして,
母平均に対する信頼区間を 100 個生成したものである."×" が標本平均を示す.左の "*" は,信頼区間
が母平均の真値 0 を含まなかった場合である.
# 平均 μ の 95 %信頼区間 100 回生成の R スクリプト
|
v <- 2; n <- 10
| # 母分散と標本の大きさ |
|
d <- qnorm(0.975)*sqrt(v/n)
| # 95%信頼区間の幅 |
|
x <- c(-2.5, -2.5, 2.5, 2.5)
| # グラフの x の範囲 |
|
y <- c(0, 100, 100, 0)
| # グラフの y の範囲 |
|
plot(x, y, type="n", xlab="", ylab="")
| # グラフ領域確保 |
|
segments(0, 0, 0, 100, col="red")
| # 母平均のライン |
|
for(i in 0:100){
| # 100回の繰り返し |
|
r <- rnorm(n, mean=0, sd=sqrt(v))
| # N(0, v)からの大きさ n の標本平均 |
|
m <- mean(r)
| # 標本平均 |
|
segments(m-d, i, m+d, i)
| # 信頼区間の表示 |
|
points(m, i, pch=4, col="red", cex=0.8)
| # 標本平均の赤×表示 |
|
if(m-d>0 || m+d<0) text(-2.5, i, "*")
| # 信頼区間が母平均を含まない(失敗)した場合 |
|
}
| # |
|
title(main="N( 0, 2 )からの大きさ 10 の標本から得られた
| |
|
平均 μ の 95 %信頼区間を 100 回作成", cex.main=1.0)
| # |
分散未知の場合の母平均 μ の区間推定
前節で考えたように正規母集団の母数が未知のときは,
大きさ n の無作為標本
x1,x2,…,xn
から,母平均 μ と母分散 σ2 は,それぞれ
標本平均 x- と標本分散 s2,
で推定される.
標本平均 x- の分布は標準化すると,
のように標準正規分布となり,標本分散に関係する量は,
のように自由度 n - 1 の χ2 分布する.これより,z と U をその自由度 n - 1 で
割った量の平方根との比は,
のように自由度 n - 1 の t 分布に従う.
自由度 n - 1 の t 分布の 97.5%分位点を t(n - 1)0.975 とすると,
t 分布する確率変数 t が -t(n - 1)0.975 から t(n - 1)0.975 に入る
確率は 0.95 となる.つまり,
となる.最後の式を母分散未知のときの母集団平均 μ の 95% 信頼区間と言う.
信頼区間の幅 d は,以下のように考えるとわかりやすい.s/√n は,標本平均 x- の
標準誤差(SE : standard error)で,推定値としての標本平均の精度を表す.標本平均がどの程度動きうる
かのざっくりとした指標が標準誤差の2倍程度(これは,正規分布の 95%幅の 1.96×標準偏差,からきている.)
であるが,正確な95%にするため,
母平均の 95% 信頼区間幅 = t(n - 1)0.975×標準誤差
にしている.
- 母分散未知の時の母平均 95% 信頼区間
上のスクリプトで,
-
m <- mean(r)
の部分の後に
-
s <- var(r)
d <- qt(0.975, df=9)*sqrt(s/n)
を入れればよい.
仮説検定(Test of hypothesis)
帰無仮説(H0)と対立仮説(H1)
統計学で扱う仮説(hypothesis)とは,母集団に対する断定や推測.たとえば,
- 母集団は正規分布に従っている.
- 母集団平均は 0 である.
- 母集団 A と母集団 B の平均は等しい.
などである.
統計的仮説検定で用いられる仮説は,まず,帰無仮説(null hypothesis)という形式で与えられる.
帰無仮説は棄却(reject)されることに意味がある仮説である.
帰無仮説と反対の仮説を対立仮説(altanative hypothesis)という.
上の3番目の例でみると,
帰無仮説:
母集団 A と母集団 B の平均は等しい.
(H0: μA = μB)
対立仮説:
母集団 A と母集団 B の平均は等しくない.
(H1: μA ≠ μB)
母集団 A と母集団 B は異なる処理(薬の投与など)をしているので,実験の目的
は,母集団 A と母集団 B の平均は異なる(処理効果がある)ことを言いたい
(対立仮説が正しいことを望む)のだが,まずは
「等しい(処理効果無し)」と仮定してみようという考え方で,
数学の背理法と似た論理である.
背理法:√2 が無理数であることを証明するため,まず√2 が有理数であると仮定し,矛盾があることを
示す.つまり,有理数であることは絶対ありえない(確率 0 である!)ことを示す.
この矛盾は,そもそも√2 を有理数とした仮定が誤っていたからであると考え,有理数という仮定を
棄却して,無理数であることを証明する.
検定の概要
検定統計量(Test statistic)
標本から算出される量で,検定に用いられるもので,t 値(t value),F 値(F value)などがある.
この値から帰無仮説を受託(accept)(採択)するか
棄却(reject)(対立仮説の採択)するかを判定する.
p 値(p value)と有意水準(Significance level)
統計的仮説検定では,たとえば2つの母集団平均が等しいという帰無仮説を考えると,
この帰無仮説のもとで,検定統計量(標本平均の差に基づく t 値など)以上
(もしくは未満)の値が得られる確率を求める.R ではこの値が p 値で表示される.
p 値は
くだけた言い方をすれば,帰無仮説が正しいとしたときに,標本のようなデータが得られる確率
である.
これが十分小さい(ほとんどありえない)ときは,平均が等しいと仮定したことが誤りであったと判断して
帰無仮説を棄却し,2つの母集団平均には差があると結論づける.
この確率がそれほど小さく
ない場合は,このような統計量が得られることもありえると考え,帰無仮説を採択し,平均が等しいと考え
てもよいとする.
棄却か採択かの判断の基準となる確率を有意水準といい,
5 % や 1 % がよく用いられる.
統計のソフトが発達していなかった頃は,検定統計量である t 値や F 値を電卓等で算出し,その値を
t 分布や F 分布の 5 %や 1 %の有意水準に対応する数表と照らし合わせて検定を行い,5 %有意とかを
記述していた.
現在では,ソフトが検定統計量に対する p 値を直接計算してくれるので数表はいらなくなった.この結果,
検定に重要な数字であった t 値や F 値より,より直接的な p 値が重要な指標になってきた.p 値を
みれば,何%有意かが一目でわかるので,結果にわざわざ 5 %有意とかを記述する必要がなくなってきており,
論文の書き方も変わってきている.
片側検定と両側検定
実験状況によっては,薬投与などの処理を行った集団(処理群)平均
μA が,薬を投与しない
集団(対照群)の平均 μB より小さくなることはないことが事前に
わかっているような場合が
ある.このようなとき,
帰無仮説,H0: μA =
μB
対立仮説,H1: μA >
μB
となる.これは,事前情報より,μA < μB となる可能性
をまったく考えない場合である.
このため検定には,片側 5 %点や 1 %点を用いる.
両側検定と信頼区間
母集団平均に対する両側検定は,母集団平均に対する信頼区間と大きな関係がある.
いま,帰無仮説(H0)と対立仮説(H1)が,
H0:μ = μ0
H1:μ ≠ μ0
であり,母分散 σ2 が既知のときを考える.
標本の大きさがnで,標本平均が x- であったとすると,母平均μに対する
95%信頼区間は,
となる.
一方,この検定の検定統計量は,標本平均の標準化値の絶対値
で,
有意水準 5 %で帰無仮説を受諾するのは,検定統計量 |z|
が両側 5 %点である 1.96 以下のときである.つまり,
|
帰無仮説を受諾 ⇔
|
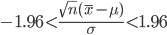
|
である.この両者の関係より,
帰無仮説を受諾 ⇔ 母平均の信頼区間に μ0 が含まれる.
帰無仮説を棄却 ⇔ 母平均の信頼区間に μ0 が含まれない.
が成り立つ
検定における2種類の過誤
検定は,仮説を棄却するか採択するかのいずれかであるが,
統計量は分布をもつので,この判定には間違いが起こることがある.
以下のように,この過誤には
2 種類がある.
統計的検定における2種類の過誤
| |
仮説の棄却(reject) |
仮説の採択(accept) |
| 仮説が真(true)のとき |
第1種の過誤(Type 1 error) |
正解 |
| 仮説が偽(false)のとき |
正解 |
第2種の過誤(Type 2 error) |
第1種の過誤が有意水準である.また,第2種の過誤の確率を β としたとき,
仮説が偽のとき正しく仮説を棄却する確率,1 - β,を検出力,もしくは検定力(power)という.
よい検定は,第1種の過誤を固定したもとで検出力の高い検定方式である.
仮説検定とまったく同一の論理構造を持ったものとして,刑事裁判があげられる.真実は,被告人
が無実か犯人かのどちらかであるが,これは本人以外は知り得ないので,裁判により無罪か有罪のいずれか
を判断する.このときの帰無仮説と対立仮説は,
-
帰無仮説(H0):被告人は無罪である(無罪推定)
対立仮説(H1):被告人は有罪である.
であり,刑事裁判でも2種類の誤りが存在する.
刑事裁判における2種類の過誤
| |
有 罪 |
無 罪 |
| 被告が無実のとき |
第1種の過誤(Type 1 error) |
正解 |
| 被告が犯人のとき |
正解 |
第2種の過誤(Type 2 error) |
人権の観点から,現在では第1種の過誤をできるだけ小さくしようとしている.このため,
いわゆる「疑わしくは罰せず」ということで,有罪に値する十分な証拠(データ)が得られらない
かぎり被告人は無罪となる.このことから,無罪≠無実であり,政治家の関わる事件をみれば
これは納得するであろう。これより,帰無仮説が棄却されず採択されたからといって,帰無仮説
が統計的に正しいという結論を出すことはできない.帰無仮説を棄却するだけの十分なデータ(証拠)
が無かったということが示されただけである.
1つの母集団に対する検定(One sample problem)
正規母集団の母平均に対する t 検定
平均 μ,分散 σ2 がともに未知である正規母集団に対して,
帰無仮説 H0: μ = μ0
対立仮説 H1: μ ≠ μ0
の両側検定を考える.
いま,母集団から大きさ n の無作為標本
x1,x2,…,xn
を抽出したところ,標本平均が x-,標本分散が s2 であったとする.
帰無仮説のもとでは,標本平均は,
と分布するので,これを,標本平均の標準誤差 s/√n で標準化した t は,
のように自由度 n - 1 の t 分布に従う.この分布の97.5%分位点を t(n - 1)0.975 とすると,
有意水準 5 %の検定は,
|t| > t(n - 1)0.975
のとき帰無仮説を棄却する.|t| が検定統計量で,この値を |t| 値という.
なお,この検定は,対のある標本に適用できる.対のある標本とは,n 組のペアー標本(paired smple),
(x1,y1 ),(x2,y2 ),
…,(xn,yn )
からなる.正規性の仮定のもとでは,
xi ~ N( μi,σx2 ),
yi ~ N( μi + δ,σy2 )
ここで興味ある母数は δ であり,μ1,…,μn は攪乱母数(nuisance parameter)
である.yi と xi の差を取ると,
zi = yi - xi →
zi ~ N( δ,σz2 )
となるので,1つの母集団に対する検定に帰着する.なおこの問題は,
反復のない 2×n の2元配置と考えて解くこともできる.
- t 検定の有意水準
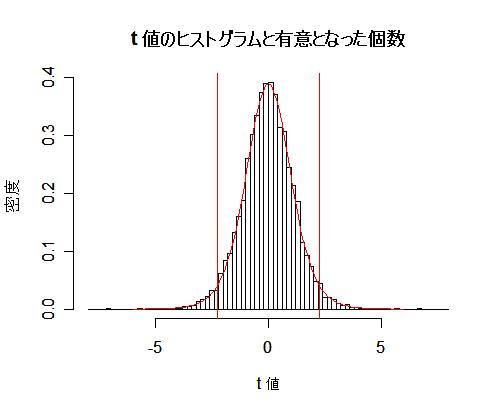
t 検定の有意水準をシミュレーションにより確認してみる.
平均 μ = 10,分散 σ2 = 4 の正規分布から大きさ n = 10 の標本を抽出し,
その標本平均 x- と標本(不偏)分散 s2 から t 値を計算する.
これを N = 10000回繰り返すと,t 値のヒストグラムができる.このヒストグラムは自由度 9 の
t 分布に従っているはずである.
帰無仮説,H0:μ = 10,
対立仮説,H1:μ ≠ 10,
の検定では,
t 値の絶対値 |t| が
自由度 9 の t 分布の97.5%分位点 t(9)0.975 より大きくなった場合に棄却される.
このため,この個数を数えれば第1種の過誤の確率,つまり有意水準がシミュレーションにより推定できる.
N = 10000回のシミュレーションでは,これがほぼ 5 %になっていた.
#t 検定の有意水準 の R スクリプト
|
N <- 10000
| # シミュレーション回数 |
|
n <- 10
| # サンプルサイズ |
|
n1 <- rnorm(N*n, mean=10, sd=2)
| # N(10, 4) から大きさ n の標本を N 回シミュレーション |
|
n1.mat <- matrix(data=n1, ncol=n)
| # データ行列 |
|
n1.mean <- apply(n1.mat, 1, mean)
| # 各サンプルの平均 |
|
n1.var <- apply(n1.mat, 1, var)
| # 各サンプルの分散 |
|
n1.var3 <- n1.var/n
| # 各標本平均の分散 |
|
n1.td <- (n1.mean - 10)/sqrt(n1.var3)
| # 各サンプルの t 値 |
|
mean(n1.td)
| # t 値の平均 |
|
sd(n1.td)
| # t 値の標準偏差 |
|
mt <- ceiling(max(abs(n1.td)))
| # t 値の絶対値の最大値 |
|
xq1 <- qt(0.025, df = (n-1))
| # t(9) の 2.5% 点 |
|
xq2 <- qt(0.975, df = (n-1))
| # t(9) の 97.5% 点 |
|
length( n1.td[abs(n1.td) > xq2])
| # 5% 検定で有意となった個数 |
|
hist(n1.td, breaks=seq(-mt, mt, by=0.2), probability=TRUE, xlab="t 値", ylab="密度", main="")
|
|
curve(dt(x, df=(n-1) ), -5,5, col="red", add=T)
| # t 分布 |
|
abline(v=xq1, col="red")
| # 採択域の下限 |
|
abline(v=xq2, col="red")
| # 採択域の上限 |
|
title(main="Histogram of t values")
| # タイトル |
問題2のヒント
n1 <- rnorm(N*n, mean=10, sd=2) # N(10, 4) から大きさ n の標本を N 回シミュレーション
のところを
n1 <- rnorm(N*n, mean=11, sd=2) # N(11, 4) から大きさ n の標本を N 回シミュレーション
に変えれば,本当は母集団は N(11, 4) だが,μ= 10 と仮定したときの棄却回数が求められる.
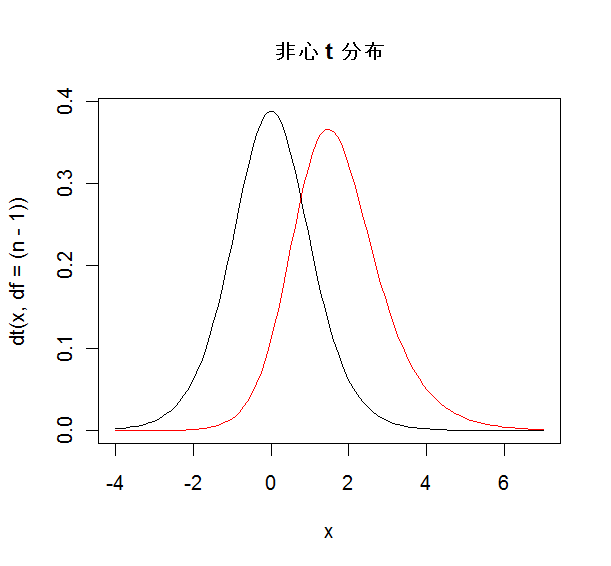
- 非心 t 分布(non-central t distribution)
帰無仮説が正しいときに,t 値の従う分布は t 分布に従うことを見た.帰無仮説が正しくない
ときに t 値の従う分布を非心 t 分布という.いま,母集団分布を N(μ,σ2) とし
たとき,
帰無仮説:H0:μ = μ0,対立仮説:H1:μ ≠ μ0
の t 検定を,大きさ n の標本で行う場合を考える.
このとき標本平均が x-,標本標準偏差が s であったとすると,
検定統計量
t = √n(x- - μ0)/s
の分布は,帰無仮説が正しくないとき,自由度 n - 1,
非心パラメーター(non-central parameter)
δ = √n(μ - μ0)/σ
の非心 t 分布に従う.この分布を用いると,t 検定の検出力を求めることができる.
# 非心 t 分布の R スクリプト
n <- 10 # サンプルサイズ
m0 <- 10 # 帰無仮説の平均
s <- 2 # 標準偏差
m <- 11 # 真の平均
delta <- sqrt(n)*(m-m0)/s # 非心度
curve(dt(x, df=(n-1)), -4,7)
curve(dt(x, df=(n-1), ncp=delta), -4,7, col="red", add=T)
title(main="non-central t distribution")
|
- t 検定の検出力(power)
前節では帰無仮説が真のとき,t 検定により仮説が棄却する確率を求めた.では,帰無仮説が偽であるとき,
帰無仮説がどれくらいの確率で正しく棄却できるであろうか.すなわち,t 検定の検出力はどの程度であろうか.
これは非心 t 分布で求められるが,シミュレーションなら比較的わかりやすく求めることができる.
後ほど問題2で検出力を求める.
ノンパラメトリック検定
ノンパラメトリック検定(nonparametric test)とは,母集団分布に関して,正規分布などのある特定の分布
を仮定しないで統計的検定を行う方法である.この手法の利点は,多少の制約がある場合もあるが,どのような
母集団分布からのデータであっても適用可能なことである.
このため,
標本中に他の観測値から飛び離れた値と思われる
異常値(outlier)が含まれているような場合でも正しい検定を与えることができる.すなわち,
頑健(robust)な検定法である.
一方,弱点としては,分布に関する情報を用いないので,特定の分布の元での最良の検定(正規母集団での小標本
に対する t 検定など)に比べ検定(検出)力(power)が低下することである.
ノンパラメトリック検定においてはデータの値を直接使わず,これを大きさの順に並べてその順位(rank)を
用いることが多い.このことは,データのもつ情報を全部使い切っていない,情報の損失があることを意味する.
他方,異常値の影響は]それだけ受けにくくなっている.
ある連続分布をもつ母集団から大きさ n の無作為標本
X1,…,Xn が抽出されたとする.ここで,母集団分布の位置母数
(location parameter)に関する両側検定問題
H0 : ξ = ξ0,H1 : ξ ≠ ξ0
および,片側検定問題
H0 : ξ = ξ0,H1 : ξ > ξ0
を考えてみよう.正規性の仮定のもとでは,Xi ~ N( ξ,σ2 ) とおき,
ξ と σ2 の推定量として標本平均 x- と標本不偏分散 s2
を用い,t 検定を行う.
ノンパラメトリック検定では,母集団の位置母数は平均でなくメディアン(中央値)で測られる.これは,
コーシー分布のように平均が存在しない分布にも対応するためである.一方,メディアン M は
と定義されるので,すべての連続分布で存在する.
さてこれからは,一般性を失うことなく ξ0 = 0 とする.ξ0 ≠ 0 のときは,
Xi のかわりに Xi - ξ0 を考えればよい.
Wilcoxon の符号順位和検定(signed rank sum test)
標本の絶対値 |X | を大きさの順に順位をつけ,これを Ri とおく.
たとえば X1 = 3.1,X2 = -4.5,X3 = 0.9 で
あったならば R1 = 2,R2 = 3,R3 = 1 で
ある.母集団は連続分布を仮定しているので,|Xi| は確率 1 ですべて互いに異なる値
をとり,Ri は一意的に定まる.
しかしながら,実際のデータでは測定精度などや測定値の丸めにより,標本の絶対値に同じ値が含まれる
ことがよくある.このような場合をタイ(tie)があるという.タイがあるときは,タイとなったデータ
の順位となり得る値の平均を順位として与えるのが普通である.
たとえば,X1 = 1.5,X2 = -0.3,X3 = 1.5,
X4 = -2.8 であったとする.X1 と X3 は順位
として 2 か 3 を取ったはずである.そこで,この値の平均 2.5 を順位として与える.この結果,
R1 = 2.5,R2 = 1,R3 = 2.5,
R4 = 4 となる.このようにすればタイのあるなしにかかわらず,
ΣRi = n(n+1)/2 となる.また,Xi = 0 というデータが
得られたときはこのデータはなかったものとして取り除いておく.
さて,Xi > 0 のときの順位和を R+,
Xi < 0 のときの順位和を R- とおき,この両者のうち小さい
方を T とおく.母集団分布が対称であるので,帰無仮説 H0 : ξ0 = 0
のもとでは R+ と R- の値はほぼ同じで,
ΣRi/2 = n(n+1)/4 に近いことが期待される.よって,T が小さいときには
帰無仮説を棄却することができる.
順列組み合わせで T の帰無仮説のもとでの分布を計算すれば,検定の有意確率が求まる.
なお,n が大きいときは,
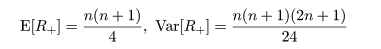
となることが知られているので,正規近似を用いて近似的な検定ができる.
- Wilcoxon の符号順位和検定の有意水準
問題1:データ数 n = 4 のとき,タイがないものとしてデータの取りえるすべての
可能性を考えることにより,T の帰無仮説のもとでの分布を出せ.
また,T = 0 のとき,帰無仮説を棄却すると決めたとすると,この検定の有意水準を求めよ.
- ヒント
-
n = 4 のとき,値の絶対値を大きさの順に並べて,X(1),X(2),
X(3),X(4),としたとき,
各 X(i) は+由来か-由来かの2通りがあるので,
24 = 16 通りの場合がある.このおのおのの場合
について T の値を出すことにより,T の確率分布が求められる.
- t 検定と符号順位和検定の検出力の比較
問題2:t 検定の有意水準の R スクリプトを参考にして,t 検定の検出力を求めよ.
- 標本の大きさ n = 10 として,帰無仮説が偽であり,
真の母集団平均が μ = 11,12,13,の3通りについて,帰無仮説;H0:μ = 10,の検定
を行った場合の
検出力(帰無仮説を棄却する割合)を求めよ.
- 真の母集団平均が μ = 11 であるとき,検出力を 90%以上にするために
必要なサンプルサイズを求めよ.
- 真の母集団平均が μ = 11 であるとき,符号順位和検定を行ったときの
検出力を 90%以上にするために
必要なサンプルサイズを求めよ.
- ヒント:ウイルコックス検定を1000回やって,p値が0.05以下の個数を出す
-
N <- 10000
n <- 10
n1 <- rnorm(N*n, mean=11, sd=2) # N(11, 4) から大きさ n の標本を N 回シミュレーション
n1.mat <- matrix(data=n1, ncol=n) # データ行列
pvalue <- NULL
for(i in 1:N){
wt <- wilcox.test(n1.mat[i,]-10)
pvalue <- c(pvalue, wt$p.value)
}
length(pvalue[pvalue<0.05])
- ラット卵巣のアスコルビン酸濃度
生物統計学入門より抜粋.ある組織抽出物が卵巣のアスコルビン酸の量を変化させるかを調べた.
ラットには左右 1 対の卵巣があるので,まず片方の卵巣を取ってアスコルビン酸濃度を測り,次に抽出物
を注射して一定時間後に残り片方の卵巣を取ってアスコルビン酸濃度(μg/1000mg 組織)を測った.8 頭の
ラットの実験結果は以下のようであった.
データダウンロード
ここで,組織抽出物はアスコルビン酸を変化させないという帰無仮説
H0 : アスコルビン酸減少量 = 0
の検定を行ってみる.
#1つの母集団に対する検定の R スクリプト
rat <- read.csv("rat.csv"); rat #データ入力
d <- rat$before-rat$after #減少量
boxplot(d, xlab="decreased concentration")
np <- length(d[d > 0]) #+の個数
nm <- length(d[d < 0]) #-の個数
binom.test(c(np,nm)) #符号検定
mean(d) #平均
sd(d) #標準偏差
t.test(d) #1標本 t 検定
t.test(rat$before, rat$after, paired=TRUE) #同じ検定
wilcox.test(d) #Wilcoxon の符号順位和検定
wilcox.test(rat$before, rat$after, paired=TRUE) #同じ検定
|
- 園芸療法の効果
園芸療法(horticultural therapy)は第2次大戦後,兵士のリハビリテーション等を通して欧米で発達してきた.
日本でも90年代から身体障害者,精神障害者,高齢者等の生活の質(QOL, Quality Of Life)や
セルフエスティーム(self-esteem,自尊感情)を向上させる手段として注目されてきていている.
園芸療法の数値的・客観的な効果の計測を行うため,認知症診断に用いられる
MSE(Mental State Examination,心理機能検査),CDT(Clock Drawing Test,時計描画テスト)と
老年者や認知症患者の日常生活の遂行能力を測る NM スケール(N 式老年者精神状態評価尺度),
N-ADL(N 式老年者日常生活動作能力評価尺度),および,気分の状態(抑うつ,活気のなさ,怒り,疲労,緊張,
混乱)を計測する POMS(Profile Of Mood State),自己記入式 QOL 質問表 QUIK を用いた.
これらの調査を園芸療法の前後でクライアントに対して行い,効果の数値的計測を行った.
ここでは,MSE の結果についての解析を行う.MSE は 30 点満点で,点数が高いほど日常生活に適応して
いると考えられている.MSE に関しては前後とも回答したクライアントの総数は 19 例であった.
データは表2にまとめられている.元データに差と符号と順位も付け加えた.このデータを用いて,園芸療法
を施す前と後では,心理機能に差がないという帰無仮説,すなわち,
H0:MSE 得点の差 = 0
の検定を行う.
データダウンロード
文献
- 鈴木修(編),大森宏,児玉良治,渡辺俊之,矢野広,山根健治(2004).
専修学校における園芸療法士教育育成システムの研究開発
(文部科学省委託平成15年度「専修学校先進的教育研究開発事業」)
- 鈴木修,渡辺俊之,矢野広,山根健治,大森宏,伊東正信,最上正秀,山下容子,小泉力,
児玉良治,頭士智美,細井薫,水口聡子,遠藤久子,樋田奈穂子,小島ユリ,郡司敏幸(2005).
福祉サービス提供者に対する園芸療法教育システムの研究開発
(平成16年度文部科学省「専修学校社会人キャリアアップ教育推進事業」)
問題3:MSE 得点データから園芸療法の効果を,符号順位和検定,t 検定を行って
検定せよ.また,クライアントの年齢を85歳以下に限定した場合の効果の検定を行い,結果の考察を行なえ.
ヒント:85歳以下を取り出すには以下のようにする.
-
mse <- read.csv("mse.csv"); mse #データ読み込み
d <- mse$after - mse$before #処方後得点-処方前得点
young <- which(mse$age < 86)
d2 <- d[young]
2つの母集団に対する検定(Two sample problem)
母平均の同等性に対する t 検定
2つの母集団 A,B があり,それぞれが平均を μA,μB,
分散を σA2,σB2 の正規分布に従って
いるが,その値は未知であるとする.いま,両集団の分散の値が等しく,
σA2=σB2=σ2,と仮定
できるとしよう.このとき,2つの母平均に対する
帰無仮説,H0: μA =
μB
対立仮説,H1: μA ≠
μB
の検定は t 分布を用いて行える.
母集団 A から大きさ nA,母集団 B から大きさ nB の標本を抽出した.
母集団 A からの標本の標本平均が x-A,
標本分散が sA2 であり,母集団 B の
標本平均が x-B,
標本分散が sB2 であった.母集団 A,B が共通の
分散 σ2 をもつとすると,その推定値 s2 は
以下のように推定できる.
|
母集団 A からの標本の偏差平方和:
|
SA=(nA-1)sA2
|
|
母集団 B からの標本の偏差平方和:
|
SB=(nB-1)sB2
|
|
母集団 A,B 全体での偏差平方和:
|
S = SA + SB
=(nA-1)sA2+
(nB-1)sB2
|
|
母集団 A,B 共通の標本分散:
|
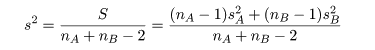
|
また,母集団Aの標本分布は,N(μA,σ2)であり,母集団Bでは,
N(μB,σ2)であることから,それぞれの標本平均は,
x-A ~ N(μA,σ2/nA),
x-B ~ N(μB,σ2/nB)
と分布する.これより,標本平均の差x-A-
x-Bは,
と分布する.
帰無仮説(H0: μA =
μB)のもとでは,μA-μB=0,なので,
標本平均の差は,
と分布する.これを標準化した z 値,
において,標準偏差 σ の代わりに標本標準偏差 s を代入した t 値が,
のように自由度 nA+nB-2 の t 分布に従うことを利用して検定ができる.
なお,母集団 A,B からの標本の大きさがともに等しく,
nA=nB=n であるときは,式がずっと簡単になる.
母集団A,Bで分散の同等性が疑われるときは,ウェルチ(Welch)の検定を用いる.
ノンパラメトリック検定
ノンパラメトリック検定においては,無作為標本 Xi,Yj がそれぞれの
累積分布関数 Fx(・),Fy(・) から抽出されたと考える.帰無仮説は,
すべての z に対して
H0 : Fx(z ) = Fy(z )
となる.
Mann-Whitney の U 検定
順位和検定(rank-sum test)とも呼ばれる.2 つの母集団分布の平均的な位置の違いを検出する方法である.
ある程度大きな標本数では t 検定の約 95% の検出効率である.
標本 X1,…,Xm,
Y1,…,Yn をまとめたものを Zi,i=1,…,m+n と
表す.すなわち,
Zi = Xi,i=1,…,m,
Zi+m = Yi,i=1,…,n
である.ここで,Z を小さいものから順に順位をつけこれを Ri とおく.もし,
タイがあったときは前節と同様に平均順位を割り付ける.ここで,
とおく.すなわち,Rx は Xi の順位の和であり,
Ry は Yi の順位の和である.
Rx + Ry = (m+n+1)(m+n)/2 である.
さて,Ux を X が Y より大きくなる個数とする.いま,
Xi の順序統計量(大きさの順に並べたもの)を,
X1',…,Xm' とし,これに対応する順位を
R1',…,Rm' とおく.明らかに X1' は
R1'-1 個の Y より大きく, X2' は
R2'-2 個の Y より大きい.同様に考えて, Xm' は
Rm'-m 個の Y より大きい.よって,
となる.同様に,
であり,Ux + Uy = mn が成立する.検定統計量 U は
Ux と Uy のうち小さい方とする.X の分布と
Y の分布が離れていれば U の値は小さくなるはずである.
m,n の値が大きいときは,式(12)の帰無仮説のもとで,
または,
となることが知られているので,正規近似を行って検定することができる.なお,この正規近似は m,n が
7 より大きければかなり正確であることも示されている.
Kolmogorov-Smirnov の 2 標本検定
累積分布関数 F(・),G(・) をもつ 2 つの母集団からそれぞれ大きさ m,n の無作為
標本 X1,…,Xm, Y1,…,Yn
が抽出されたとする.このとき,
を経験(標本)累積分布関数という.標本 Yi に対する経験累積分布関数を
Gn(x ) としたとき,2 つの母集団からの経験累積分布の最大偏差
を求める.次に,
を求め,これを検定統計量として用いる.
2 つの母集団の累積分布関数が等しいという帰無仮説のもとでの K の漸近分布
(m,n → ∞ としたときの分布)から以下で定義される臨界値が求められている.すなわち,
であり,この値は以下の表に示されている.
表.Kolmogorov-Smirnov 2 標本両側検定の臨界値
| 確率:γ |
0.99 | 0.95 | 0.90 |
0.85 | 0.80 |
| 臨界値:kγ |
1.63 | 1.36 | 1.22 |
1.14 | 1.07 |
2つの母集団分散の同等性の検定
2つの母集団 A,B があり,それぞれが平均を μA,μB,
分散を σA2,σB2 の正規分布に従って
いるが,その値は未知であるとする.このとき,2つの母分散の同等性の検定,
帰無仮説,H0: σA2 =
σB2
対立仮説,H1: σA2 ≠
σB2
の検定を考える.
母集団 A から大きさ nA,母集団 B から大きさ nB の標本を抽出した.
母集団 A からの標本の標本平均が x-A,
標本分散が sA2 であり,母集団 B の
標本平均が x-B,
標本分散が sB2 であるとする.すると,
標本分散に関係した量はそれぞれ
と χ2 分布に従い,それぞれが独立である.これらの量の比は,
のように,自由度 nA - 1,nB - 1 の F 分布に従う.
ところで,帰無仮説が正しいとする
と,σA2 = σB2 とおけるので,
母集団の分散比は,γ0 = σA2/σB2 = 1,
となる.このとき,標本分散の分散比の統計量 γ が,
と,自由度 nA - 1,nB - 1 の F 分布に従うので,この γ 値を検定統計量にして
2つの母分散が等しいという帰無仮説の検定が行える.
すなわち,有意水準 5 %の検定を行うには,自由度 nA - 1,nB - 1 の F 分布
の 2.5%点と 97.5%点をそれぞれ F(nA - 1,nB - 1)0.025,
F(nA - 1,nB - 1)0.975 とすると,検定統計量 γ が,
γ < F(nA - 1,nB - 1)0.025,
γ > F(nA - 1,nB - 1)0.975,
のいずれかの不等式を満たしたとき帰無仮説を棄却し,2つの母集団の分散は有意に異なると結論づける.
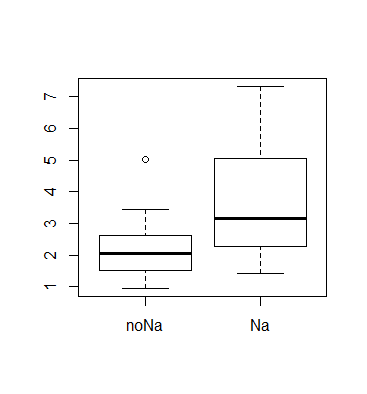
- 淡水性ウナギデータの解析
淡水性ウナギの汽水域での生理活性の違いのデータ
を2標本データとして違いを検定してみよう.ただし,2母集団で分散の違いがあるようなので,まず,
分散の同等性の検定を行い,違いが認められるときは,データの対数変換(lx <- log(x))を行うなどして,分散安定化
変換を行って t 検定を行ってみる.また,データの対数変換などを行わず.ウェルチ検定やノンパラメトリック
検定を行った場合との比較検討を行う.
データダウンロード
分散同等性の検定をやってみる.
-
unagi <- read.csv("unagi2.csv")
attach(unagi)
boxplot(unagi)
var.test(noNa, Na)
分散同等性検定で,p 値 = 0.047 で有意に分散が異なっていることがわかったので,
通常の t 検定を行うことはできない.
t.test(noNa, Na)
wilcox.test(noNa, Na)
ks.test(noNa, Na)
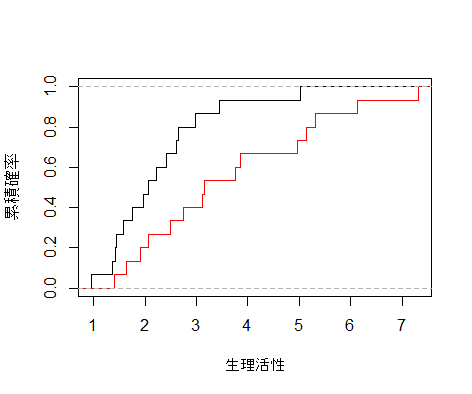
plot(ecdf(noNa), do.points=F, verticals=T,xlab="生理活性", ylab="累積確率",
xlim=range(noNa, Na), main="")
plot(ecdf(Na), do.points=F, verticals=T, add=T, col.h='red', col.v='red')
| 検定方法 | p 値 | |
|---|
| 分散同等性検定 | 0.047 | * |
|---|
| Welch 検定 | 0.01355 | * |
|---|
| 順位和検定 | 0.01452 | * |
|---|
| Kolmogorov-Smirnov 検定 | 0.07546 | |
|---|
Kolmogorov-Smirnov 検定以外では5%有意となり,ウナギの生理活性は淡水と汽水で有意に異なっていた.
なお,Kolmogorov-Smirnov 検定の検出力は低いことがわかる.
分散安定化変換を試す.
x <- log(noNa)
y <- log(Na)
boxplot(x, y)
var.test(x, y)
t.test(x, y, var.equal=T)
| 検定方法 | p 値 | |
|---|
| 分散同等性検定 | 0.5071 | |
|---|
| t 検定 | 0.01126 | * |
|---|
分散安定化変換を行ったところ,分散の同等性は棄却されず,普通の t 検定を行った.
昔の指針:2つの母集団の分散の均質性が疑われるときは分散の同等性の検定を行い,これが棄却された
ときは仕方なく Welch 検定(自由度の計算が面倒で,小数点自由度のときは t 分布表の線形補間で97.5%を計算
する)を行う.
今の指針:最初から Welch 検定でよいのでは.
問題4:園芸療法の MSE 得点データを,園芸療法を行わなかった対照区 19 名と園芸療法を処方
した処理区 19 名のデータとみなし,t 検定,Mann-Whitney の U 検定,
Kolmogorov-Smirnov 検定を行え.
また,クライアントの年齢を85歳以下に限定した場合の効果の検定を行い,結果の考察を行なえ.
分割表の解析
成功確率(比率)の同等性の近似検定
成功確率 px のベルヌイ試行を n 回行ったときの成功回数を X,
成功確率 py のベルヌイ試行を m 回行ったときの成功回数を Y とする.このとき,
2つの成功確率が等しいかどうか,すなわち,
帰無仮説,H0: px = py,
対立仮説,H1: px ≠ py,
の検定を考える.帰無仮説のもとでは,px = py = p とおけるので,
px の推定量である X/n と py の推定量である Y/m の
平均と分散は,それぞれ
となる.これより,X/n - Y/m の帰無仮説のもとで平均と分散は,
となるので,これをその平均を引いて標準偏差で割って標準化した z は,
のように漸近的に標準正規分布に従う.
ところで,帰無仮説のもとでの成功確率 p は,Y と Y をこみにして,
と推定されるので,これを z に代入すれば,
となり,T = |z| を検定統計量にして,たとえば,T > 1.96 のとき帰無仮説を棄却すれば,
近似的な有意水準 5%の検定が行える.
なお,連続性の補正を入れた検定統計量は,
となる.
2×2分割表
成功確率 px の試行 X では a 回成功し,
b 回失敗したが,別の成功確率 py 試行 Y では c 回成功,d 回失敗であったとする.このとき,
試行 X と試行 Y で成功確率が等しいという,
帰無仮説,H0: px = py,
対立仮説,H1: px ≠ py,
の検定を考える.
このようなデータは,
2 × 2 分割表データ
| | 成 功 | 失 敗 | 計 |
|---|
| 試行 X |
a | b | a + b |
|---|
| 試行 Y |
c | d | c + d |
|---|
| 計 |
a + c | b + d | N |
|---|
とまとめられる.ただし,N = a + b + c + d,である.
これを2×2分割表という.各試行の成功回数と失敗回数を記録した部分をセル,その外側の
「計」に対応する部分を周辺度数という.
周辺度数を固定したときに,帰無仮説のもとでの各セル期待度数は,
帰無仮説のもとでの期待度数
| | 成 功 | 失 敗 |
|---|
| 試行 X |
(a + b)(a + c)/N | (a + b)(b + d)/N |
|---|
| 試行 Y |
(c + d)(a + c)/N | (c + d)(b + d)/N |
|---|
となる.ここで,ピアソン(Pearson)のχ2 値,
を計算する.連続性の補正を入れると,
である.このとき,
Na - (a + b)(a + c) = (a + b + c + d)a - (a2 + ab + ac + bc) = ad - bc
という関係を利用すると,
2×2分割表の χ2 値は,
と計算される.
ところで,比率の同等性検定の z において,X = a,Y = c,n = a + b,m = c + d,
m + n = N,とおきかえると,
となり,z2 値が χ2 値と同じであることがわかる.これより,
と分布するので,自由度 1 の χ2 分布を利用して,成功確率の同等性の検定を行うことができる.
また,χ2 値に連続性の補正を行うときは,
とする.
- 勝率同等性の χ2 検定
# 勝率同等性ピアソン χ2 検定の R スクリプト
|
shogi <- c(21, 9)
| # A の将棋の勝ち負け数 |
|
igo <- c(12, 18)
| # A の囲碁の勝ち負け数 |
|
x <- rbind(shogi, igo)
| # 行連結による行列化 |
|
chisq.test(x, correct=F)
| # 勝率同等性 χ2 検定(連続性の補正なし) |
|
chisq.test(x)
| # 勝率同等性 χ2 検定(連続性の補正) |
Fisher の直接確率法
試行回数が少ないときは,各セルの期待度数が小さくなるので,近似の精度はよくない.2×2 分割表では,
一般に期待度数が 5 以下のセルがあると χ2 検定は適当でないと言われている.
このようなときは,周辺度数を固定して,データの表が得られる確率より小さな場合をすべて足し合わせて有意
確率(p 値)を計算する.
前節の囲碁と将棋の例で、勝率はそのままで試合回数を10試合にしてセルの頻度が小さくなった場合で
説明する.データを 2 × 2 分割表でまとめると以下のようになる.
将棋と囲碁 2 × 2 分割表
| | 勝 ち | 負 け |
計 | 場合の数 |
|---|
| 将 棋 |
7 | 3 |
10 | 10C7 |
|---|
| 囲 碁 |
4 | 6 |
10 | 10C4 |
|---|
| 計 |
11 | 9 |
20 | 20C11 |
|---|
上の表で,勝ち負けがゲームの種類に関係ないすると,この表ができる確率は,
p = 10C7×10C4
/20C11 = 0.15004
となる.
次に,周辺度数を固定した場合できる可能性のある表をすべて数えあげ,
勝敗がランダムなときの表が
生成する確率を計算すると以下のようになる.
| パターン1 | 勝ち | 負け |
計 | 場合の数 |
| 将 棋 | 8 | 2 |
10 | 10C8 |
| 囲 碁 | 3 | 7 |
10 | 10C3 |
| 計 | 11 | 9 |
20 | 20C11 |
| 確 率 |
10C8×10C3
/20C11 = 0.03215 |
|
|
| パターン2 | 勝ち | 負け |
計 | 場合の数 |
| 将 棋 | 9 | 1 |
10 | 10C9 |
| 囲 碁 | 2 | 8 |
10 | 10C2 |
| 計 | 11 | 9 |
20 | 20C11 |
| 確 率 |
10C9×10C2
/20C11 = 0.00268 |
|
|
| パターン3 | 勝ち | 負け |
計 | 場合の数 |
| 将 棋 | 10 | 0 |
10 | 10C10 |
| 囲 碁 | 1 | 9 |
10 | 10C1 |
| 計 | 11 | 9 |
20 | 20C11 |
| 確 率 |
10C10×10C1
/20C11 = 0.00006 |
|
| |
| パターン4 | 勝ち | 負け |
計 | 場合の数 |
| 将 棋 | 6 | 4 |
10 | 10C6 |
| 囲 碁 | 5 | 5 |
10 | 10C5 |
| 計 | 11 | 9 |
20 | 20C11 |
| 確 率 |
10C6×10C5
/20C11 = 0.315075 |
|
|
| パターン5 | 勝ち | 負け |
計 | 場合の数 |
| 将 棋 | 5 | 5 |
10 | 10C5 |
| 囲 碁 | 6 | 4 |
10 | 10C6 |
| 計 | 11 | 9 |
20 | 20C11 |
| 確 率 |
10C5×10C6
/20C11 = 0.315075 |
|
|
| パターン6 | 勝ち | 負け |
計 | 場合の数 |
| 将 棋 | 4 | 6 |
10 | 10C4 |
| 囲 碁 | 7 | 3 |
10 | 10C7 |
| 計 | 11 | 9 |
20 | 20C11 |
| 確 率 |
10C4×10C7
/20C11 = 0.15004 |
|
| |
| パターン7 | 勝ち | 負け |
計 | 場合の数 |
| 将 棋 | 3 | 7 |
10 | 10C3 |
| 囲 碁 | 8 | 2 |
10 | 10C8 |
| 計 | 11 | 9 |
20 | 20C11 |
| 確 率 |
10C3×10C8
/20C11 = 0.03215 |
|
|
| パターン8 | 勝ち | 負け |
計 | 場合の数 |
| 将 棋 | 2 | 8 |
10 | 10C2 |
| 囲 碁 | 9 | 1 |
10 | 10C9 |
| 計 | 11 | 9 |
20 | 20C11 |
| 確 率 |
10C2×10C9
/20C11 = 0.00268 |
|
|
| パターン9 | 勝ち | 負け |
計 | 場合の数 |
| 将 棋 | 1 | 9 |
10 | 10C1 |
| 囲 碁 | 10 | 0 |
10 | 10C10 |
| 計 | 11 | 9 |
20 | 20C11 |
| 確 率 |
10C1×10C10
/20C11 = 0.00006 |
|
この中でデータのような表が得られる確率と同じかそれより小さな確率をすべて加え合わせたものが,
p 値である.すなわち,パターン1,パターン2,パターン3,パターン6,パターン7,パターン8,
パターン9,の確率を加え合わせる.
特に,上側確率が,データとパターン1,パターン2,パターン3,を加えたもので,
上側確率:Pupper = 0.15004 + 0.03215 + 0.00268 + 0.00006 = 0.1849
であり,下側確率が残りのパターンの確率を加え,
下側確率:Plower = 0.15004 + 0.03215 + 0.00268 + 0.00006 = 0.1849
となる.p 値(有意確率)は,これを加え,
p 値:Pupper + Plower = 0.1849 + 0.1849 = 0.3698
となる.
- 勝率同等性の Fisher 直接確率法検定
-
shogi <- c(7, 3) # A の将棋の勝ち負け数
igo <- c(4, 6) # A の囲碁の勝ち負け数
x <- rbind(shogi, igo) # 行連結による行列化
m <- sum(shogi) # 将棋の勝負回数
chisq.test(x) # 勝率同等性 χ2 検定.警告が出る.
fisher.test(x) # 勝率同等性 Fisher 直接確率
- 超幾何分布による Fisher 直接確率法検定の p 値
ところで,
将棋を m = 10 回,囲碁を n = 10 回勝負し,全部で k = 11 回の「勝ち」があったとき,将棋では
x 回の「勝ち」が得られる確率分布は,超幾何分布 f(x; m, n, k) に従う.
超幾何分布で x = 7 回の「勝ち」が得られる確率以下である確率をすべて加え合わせたのが
p 値となる.
問題5:勝敗の比率はそのままで,試行回数を増やした(n,m = 30)ときの
勝率同等性 Fisher 直接法の p 値を,超幾何分布の確率密度関数
dhyper(x, m, n, k) か累積分布関数 phyper(x, m, n, k)
用いて算出せよ.
クロス集計と独立性の検定
n 標本を2つの変数 A,B で分類したとき,2つの変数に関連があるかを調べたい.
変数 A を集団属性(集団1,集団2),変数 B を反応パターン(反応1,反応2)とした
とき,データは以下のようにまとめられる.これをクロス集計と呼ぶ.
2 × 2 分割表データ
| | 反応1 | 反応2 | 計 |
|---|
| 集団1 | n11 |
n12 |
n1・ |
|---|
| 集団2 | n21 |
n22 |
n2・ |
|---|
| 計 | n・1 |
n・2 |
n |
|---|
ここで,nij は,集団 i の標本の中で,反応 j を取った人数(度数)
である.また,ni・ は集団 i の標本の大きさで,
n・j は標本全体(大きさ n)の中で反応 j を取った人数
を表し,それぞれ周辺度数という.
このような表において,集団で反応パターンに違いがなければ,集団 i で反応 j を取る確率は,
集団 i である確率 ni・/n に
集団 j である確率 n・j/n をかけた
ni・n・j/
n2 となることが期待される.これより,
集団 i で反応 j を取る人数(度数)は,
ni・n・j/n
となることが期待される.これを独立性の仮定という.
いま,集団 i の標本の中で,反応 j を取る確率を pij とし,集団 i の周辺確率を pi.,
反応 j の周辺確率を p.j とすると,独立性の仮説は,
帰無仮説,H0: pij = pi.p.j,
対立仮説,H1: pij ≠ pi.p.j,
の検定になる.
帰無仮説のもとで,表現は違うが前節とまったく同じ χ2 値が,
と分布するので,独立性の検定を行うことができる.連続性の補正も前節とまったく同じようにして行う.
すなわち,比率の同等性の検定と独立性の検定は,意味が違うが検定のやり方はまったく同じである.
オッズ比(odds ratio)
変数 A,B 間の関連の強さを測る指標としてオッズ比がある.
たとえば,食中毒事件が起きたとき,
食中毒症状が出たか出なかったか(変数 A)を
出された食材を食べた人と食べなかった人(変数 B)で
分類する.このとき,ある食材に対しての分類は以下のようであったとする.
| | 発症あり(A1) | 発症なし(A2) |
|---|
| 食べた(B1) | a | b |
|---|
| 食べなかった(B2) | c | d |
|---|
食材を食べたときに発症する確率 Pr[A1| B1] の推定値は a/(a + b),
発症しない確率 Pr[A2| B1] の推定値は b/(a + b) である.
これより,その食材を食べたとき食中毒を発症する危険率(オッズ)は,
Pr[A1| B1]/P[A2| B1] = a/b
であり,同様に食べなかったときの発症オッズは,
Pr[A1| B2]/P[A2| B2] = c/d
である.この両者の比,
をオッズ比といい,ある食材を食べたことが食中毒症状発症にどれだけ危険であるかの尺度になる.
危険が同等のときは,オッズ比は 1 となる.すなわち,オッズ比が 1 より有意に大きいときは食中毒
リスクの高かった食材(食中毒原因食材)になり,
1 より有意に小さいときは食中毒リスクを軽減させた食材となる.
なお,どこかのセルデータが 0 であったときは,
セルのすべての値に 0.5 を加えて補正する.
ところで,R の fisher.test() では,超幾何分布に基づいてオッズ比の最尤推定を
行っているらしいので,上の式の単純な推定値とは値が多少異なっているが,ソースの解読を
していないので詳細は不明である.
ピアソン χ2 検定は,
帰無仮説 H0:オッズ比 φ = 1
の検定と同等である.
- 心筋梗塞死亡率の χ2 独立性検定とオッズ比
ある病院で,心筋梗塞発作後の6ヶ月以内の死亡率と
牛乳に対する抗体を持った患者と持っていない患者でまとめたのが下の表である.
心筋梗塞死亡リスクと牛乳に対する抗体の有無との関連を調べる.
心筋梗塞死亡率と牛乳に対する抗体の有無
| | 6ヶ月以内死亡 | 6ヶ月生存 |
|---|
| 牛乳に対する抗体あり | 29 | 71 |
|---|
| 牛乳に対する抗体なし | 10 | 94 |
|---|
# 心筋梗塞死亡率の R スクリプト
x <- matrix(c(29, 71, 10, 94), nrow=2, byrow=T); x
chisq.test(x) # χ2 値,p 値
fisher.test(x) # オッズ比,p 値
|
- 食中毒原因食材の χ2 独立性検定とオッズ比
1940 年のNew York 州 Oswego の協会の夕食会における胃腸炎異常発生の喫食
調査データによると食材と食中毒症状とで以下の関係があった.
詳しいデータ
| 食品名 | 発症あり | 発症なし |
|---|
| 食べた | 食べない | 食べた | 食べない |
|---|
| ケーキ | 27 | 19 |
13 | 16 |
|---|
| ハムステーキ | 29 | 17 |
17 | 12 |
|---|
| バニラアイス | 43 | 3 |
11 | 18 |
|---|
| チョコアイス | 25 | 20 |
22 | 7 |
|---|
| フルーツサラダ | 4 | 42 |
2 | 27 |
|---|
問題6: 食材ごとの発症データから,χ2 独立性検定とオッズ比を使って
食中毒の原因食材を推定せよ.すなわち,オッズ比が 1 より有意に大きくなった食材が食中毒の
原因食材と特定できる.オッズ比が 1 より小さな食材は食中毒発生を抑制した食材である.
このような食材があった場合,どうして抑制効果があったのか考察せよ.
参考文献(古い順)
- Introduction to the Theory of Statistics, Mood, A. M., Graubill, F. A. & Boes, D. C., 1974,
McGRAW-HILL
- 「実験」生産環境生物学,東京大学大学院農学生命科学研究科生産・環境生物学専攻編,1999,朝倉書店
- 工学のためのデータサイエンス入門-フリーな統計環境Rを用いたデータ解析-,間瀬茂ら,2004,
数理工学社
- 実践生物統計学-分子から生態まで-(第 1 章,第 2 章),
東京大学生物測定学研究室編(大森宏ら),
2004,朝倉書店
- The R Tips データ解析環境 R の基本技・グラフィックス活用集,船尾暢男,2005,九天社
- R で学ぶデータマインニング I -データ解析の視点から-,熊谷悦生・船尾暢男,2007,九天社
- R で学ぶデータマインニング II -シミュレーションの視点から-,熊谷悦生・船尾暢男,2007,九天社
Copyright (C) 2008, Hiroshi Omori. 最終更新日:2015年9月24日
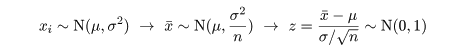
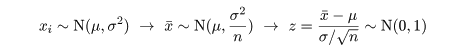
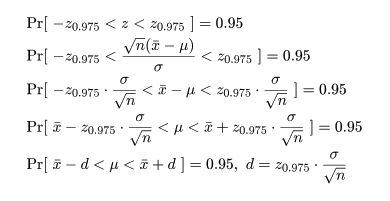

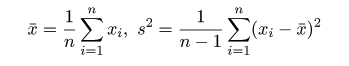
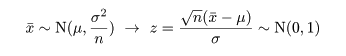
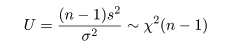
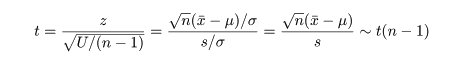
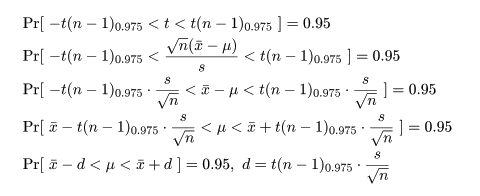
![{\rm Pr} \Bigl[ -1.96 < \frac{\sqrt{n}(\bar{x}-\mu)}{\sigma} < 1.96 \Bigr] = 0.95](images4/EXTERN_0005.png)
![{\rm Pr} \bigl[ \bar{x} - 1.96 \cdot\frac{\sigma}{\sqrt{n}} < \mu < \bar{x} + 1.96 \cdot\frac{\sigma}{\sqrt{n}} \Bigr]](images4/EXTERN_0006.png)