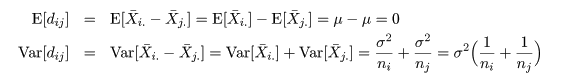
y = x +δ+ e
とおける。ただし、δは偏り(バイアス)、e は測定誤差で、 その分散 Var[e] =σe2 とする。 バイアスは計測方法の「くせ」による系統的な誤差値で、 真の値を過大評価もしくは過少評価したりする傾向がある時に現れる。
E[y] = E[x] +δ+ E[e] = μ+δ
Var[y] = Var[x] + Var[e]
= σ2 + σe2
data <- read.csv("data.csv")
head(data)
bx <- levels(data$brand)
bag <- rep(0, nrow(data)) # bag というデータ(ブランドごとに1,2を付与)
for(j in 1:length(bx)){
v <- which(data$brand==bx[j])
bag[v] <- c(rep(1,15), rep(2,15))
}
bag <- factor(bag)
data <- data.frame(data, bag)
head(data)
attach(data) # dataの使用を宣言
brand_group <- paste(brand, group, sep=":")
# ブランド、班ごとの標準偏差。
# 標準偏差が小さい測定方法が望ましい。
res1 <- tapply(ruler, brand_group, sd, na.rm = T); res1 # ものさし
mean(res1) # ものさしの標準偏差の平均
# バイアスを見るため、ブランド、班ごとの平均を見る。
# 理想的には同じブランドを計測した2班が平行直線になっているのが望ましい。
# 上下にぶれるのは良くない計測方法である。
# また、青と赤は同じブランドの異なる2袋なので値はほぼ同じであると考えられる。
levels(brand)
# donki
bx <- "donki"
v <- which(brand==bx)
y <- data[v,]
a <- unique(y$group)
m1 <- apply(y[bag[v]==1, 3:6], 2, mean, na.rm=T)
m2 <- apply(y[bag[v]==2, 3:6], 2, mean, na.rm=T)
plot(1:4, m1, type="n", xaxt="n", xlab="", ylab="Length", ylim=range(c(m1,m2)))
axis(side=1, at=1:4, labels=names(m1))
lines(1:4, m1, type="b", col="red")
lines(1:4, m2, type="b", col="blue")
legend("topleft", legend=a, pch=1, col=c("red","blue"))
title(main=paste("Mean length of", bx, sep=" "))
detach(data) # dataの使用終了
Xijk=μ+αi+βij+eijk、
とおける。ここで、μは総平均、αi はブランドの効果、 βij は ブランドごとの袋の効果、eijk は誤差項で、 eijk 〜 N (0, σ2) を仮定する。 このようにブランド(主効果)ごとに標本の単位(袋)があり、この単位(袋)の中に 個体があるようなモデルをネスト(枝分かれ)分散分析 (Nested Analysis of Variance)という。Xij=μ+αi+eij、j = 1,…,30
のようにする。これは、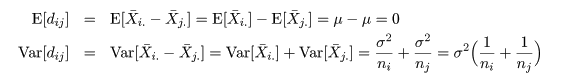
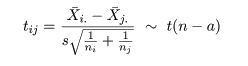
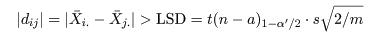
attach(data) # dataの使用を宣言 value <- nogisu boxplot(value ~ bag:brand) # "donki" 内での袋間の違いの検定 v <- which(brand=="donki") t.test(value[v] ~ bag[v]) # ネスト分散分析 # ブランド、袋間の検定 summary(aov(value ~ brand/bag)) # ブランド間の検定 # 警告メッセージは無視してよい。 summary(aov(value ~ brand + Error(brand:bag))) # ブランド内袋データを一緒にする。 boxplot(value ~ brand) summary(fm <- aov(value ~ brand)) # 多重比較 pairwise.t.test(value, brand, pool.sd = FALSE) # Tukey の HSD TukeyHSD(fm, "brand") plot(TukeyHSD(fm, "brand")) detach(data) # dataの使用終了
xA - xB 〜 N(a - b, 1)
という正規分布に従う。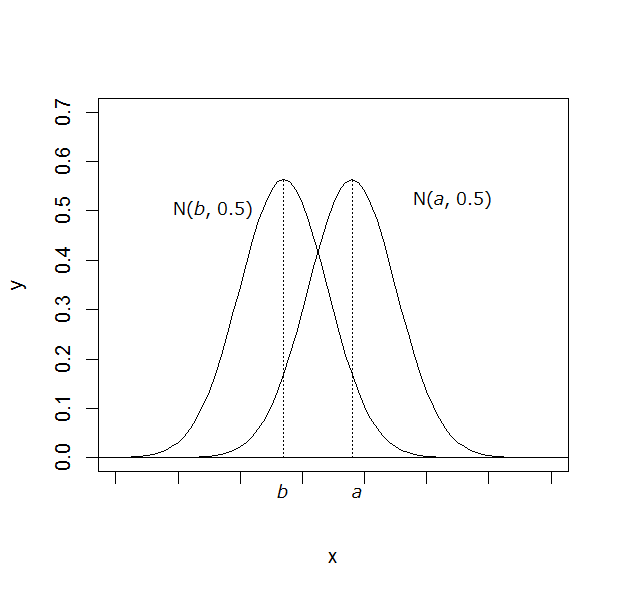 |
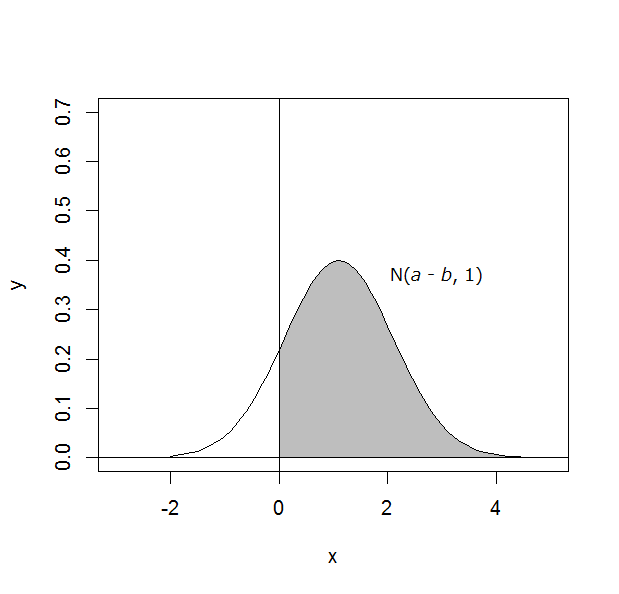 |
qnorm(0.85) = 1.036 → a - b = 1.036, a + b = 0 → a = 0.518, b = -0.518
と推定できる。
| A | B | C | D | E | |
|---|---|---|---|---|---|
| A | 0 | 9 | 7 | 7 | 6 |
| B | 1 | 0 | 5 | 3 | 4 |
| C | 3 | 5 | 0 | 7 | 6 |
| D | 3 | 7 | 3 | 0 | 4 |
| E | 4 | 6 | 4 | 6 | 0 |
A <- c(0, 9, 7, 7, 6)
B <- c(1, 0, 5, 3, 4)
C <- c(3, 5, 0, 7, 6)
D <- c(3, 7, 3, 0, 4)
E <- c(4, 6, 4, 6, 0)
thurs <- rbind(A,B,C,D,E)
colnames(thurs) <- c("A","B","C","D","E")
diag(thurs) <- NA
thurs <- thurs/10
thurs
qn_thurs <- qnorm(thurs)
x <- apply(qn_thurs, 1, mean, na.rm=T)
sort(x, decreasing=T)
thurs2 <- thurs thurs2[2,1] <- thurs2[4,2] <- thurs2[4,3] <- thurs2[5,1] <- thurs2[5,3] <- NA thurs2[1,2] <- thurs2[2,4] <- thurs2[3,4] <- thurs2[1,5] <- thurs2[3,5] <- NA thurs2 qn_thurs2 <- qnorm(thurs2) x2 <- apply(qn_thurs2, 1, mean, na.rm=T) sort(x2, decreasing=T)