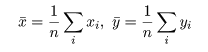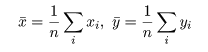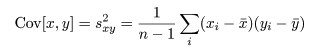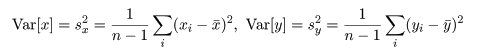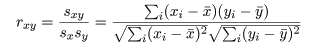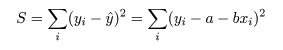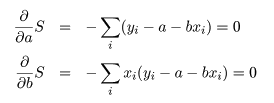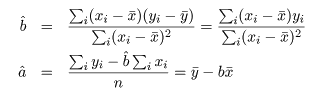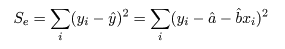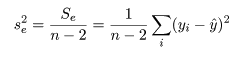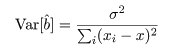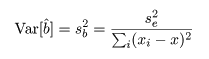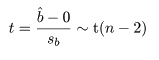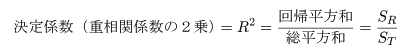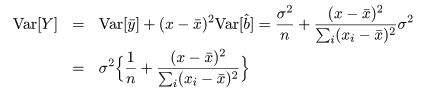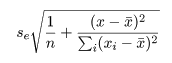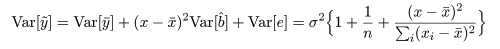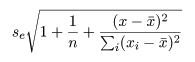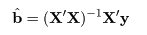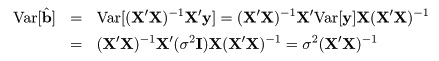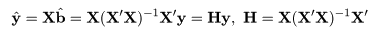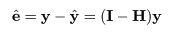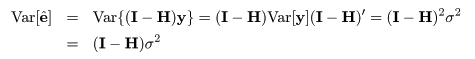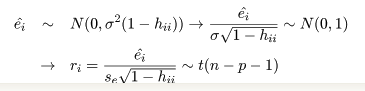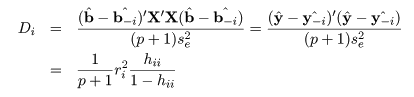2014年生物測定基礎実験
統計解析5
東京大学大学院農学生命科学研究科 大森宏
この実験の目的
統計解析ソフトRを用いて,統計解析の理論と実践を学ぶ
回帰分析(Regression Analysis)
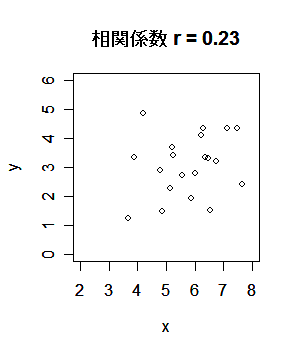
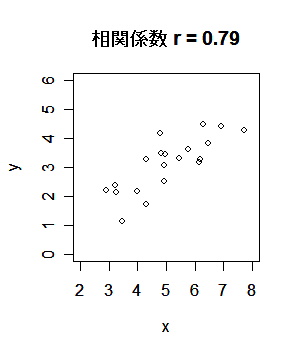
相関
標本(サンプル)に対し,2つの変数 x,y が測定されているとする.
たとえば,x が身長(m)であり,y が体重(kg)である.
大きさ n の標本(サンプル)に対し,2つの変数の組のデータが,
(x1 ,y1 ),
(x2 ,y2 ),
…,
(xn ,yn )
であったとする.
変数間の関連性の強さを測る量として共分散(Covariance),Cov[x ,y ] がある.
これは,変数に対する平均を,
として,
と定義される.
共分散は測定単位により大きさが変わるので,これをおのおのの変数の標本分散,
Var[x],Var[y],
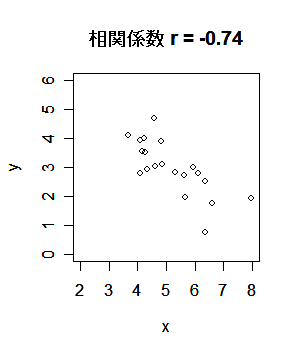
で標準化したものがピアソン(Peason)の積率
相関係数 r,-1≦r≦1,であり,
と定義される.これは,変数間の線形的関係の強さ,
(x が大きいと y も大きく,x が小さいと y も小さい,)
を測る指標で,|r|=1 のときは,
変数 x,y は完全な直線関係にあり,r =0 のときは,線形的な関係
がない.r が 1 に近いときは,正の相関関係があるといい,
r が -1 に近いときは,負の相関関係があるという.
- 入試得点とその後の成績
入試得点とその後の成績には相関が強いのではないかと考えられるが,実際に測ってみるとそれほどでもないことが多い.
このことから,入試を行うことを疑問視する人も出てくる(入試得点と成績に相関がないのだから,入試を
行うことに意味がない).しかしながら入試では,多くの学生が入学できないので,本来入学していたら
取れたであろう成績のデータが欠測していると考えるべきである.
統計学的には以下のように考えればよい.いま,入試得点(x)とその後の成績(y)に r の相関があるとする.
そして,x と y は相関 r を持つ 2 変量正規分布に従うとする.しかし現実には,
入試得点の低い者(x < x0)は入学できないので,
この 2 変量正規分布を x = x0 で切断(truncate)した分布のみが観測される.
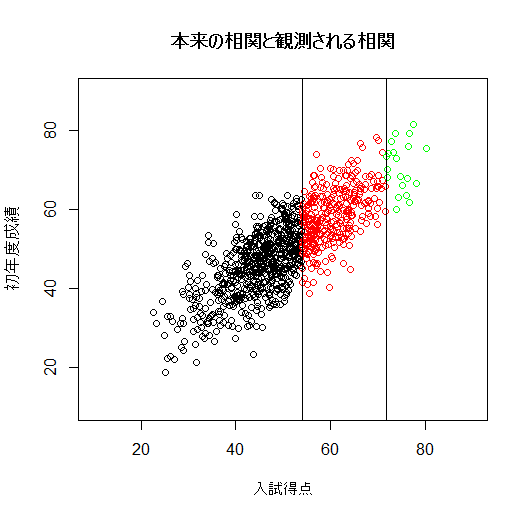
いま,入試得点(x)と成績(y)がそれぞれ,平均 50,分散 100(標準偏差 10),相関 0.8 を持つ 2 変量
正規分布とし,合格ラインは x = 54 点であるとする.
1000人の志願者があったとすると,x ≧ 54 である 330 名程度が合格するので,
競争倍率約3倍の試験である.
また,特待生の募集枠が20人であるとき,試験の上位20名を特待生としたとき
の入試得点とその後の成績の相関を求めてみる.
# 入試得点と成績の R スクリプト
library(MASS) # MASS ライブラリーの読み込み
s <- matrix(c(100, 80, 80, 100), nrow=2); s # 分散共分散行列の定義
x <- mvrnorm(1000,c(50,50),s) # 平均 50,分散 s の 2 変量正規分布乱数 1000 個生成
plot(x, xlab="入試得点", ylab="初年度成績") # 分布全体を表示
points(x[x[,1]>54,], col="red") # 入学者のみ赤で表示
1000/nrow(x[x[,1]>54,]) # 競争率
xs1 <- sort(x[,1], decreasing=T) # 入試得点を大きさの順に並べ替え
xb1 <- (xs1[20]+xs1[21])/2; xb1 # 特待生合格ライン
points(x[x[,1]>xb1,], col="green") # 入学者のみ赤で表示
abline(v=54) # 合格ライン
abline(v=xb1) # 特待生合格ライン
title(main="本来の相関と観測される相関") #
cor(x)[1,2] # 本来あるべき相関
cor(x[x[,1]>54,])[1,2] # 実際に観測される相関
cor(x[x[,1]>xb1,])[1,2]
|
直線回帰
モデル
2つの変数 x ,y に対し,y の値が x の値の動きにつれて
線形的に変化すると仮定される,つまり,
y = a + b x
という関係が成り立っていると考えられる場合である.これを y の x に
対する直線回帰といい,a ,b を回帰係数という.
また,変数 y を従属変数,目的変数といい,変数 x を独立変数,説明変数と
いう.
最小2乗法
データに最もよくあてはまる直線回帰式を得るには,データ点
(xi ,yi ),
と回帰による推定点,
(xi ,y^i ),
y^i = a + b xi ,
の間の距離の2乗和 S が最小になるような回帰係数 a ,b を求める.つまり,
を最小化する a ,b を求める問題に帰着する.これを最小2乗法という.
これは,S を a ,b で偏微分して 0 とおくことによって得られる.つまり,
の連立方程式を a ,b で解けばよい.これより,回帰係数の推定値 a^,
b^ が,
と得られる.
回帰式の統計モデル
推定された直線回帰式がどの程度現実のデータに適合しているかを調べるために,
回帰式が従う統計モデルを考える.標本の格データ点,
(xi ,yi ),
が,
yi = a +
b xi +
ei ,
ei
〜 N( 0,σ2 )
であると仮定する.ei は誤差(error),あるいは,
残差(residual)で,直線回帰
式では説明がつかない部分を表し,これが互いに独立に平均 0,分散 σ2
の正規分布に従うと仮定する.誤差の大きさが大きいときは,直線回帰式ではデータが説明できない
と考える.
残差分散と回帰係数の標準誤差
回帰で説明がつかない残差平方和 Se は,
で求められる.これの自由度は n−2 であるので(2つの回帰係数分の自由度を除く),回帰の
残差(誤差)分散の推定値は,
で求められる.
一般に,Var(yi )
= σ2 であるとき,その定数(c)
倍の分散は,
Var(cyi ) = c2σ2,
Var(Σici
yi ) =
Σici
2 σ2
であり,従属変数 y のデータ yi は,
yi
〜 N( a + b xi ,σ2 )
と分布するので,回帰係数の推定値 b^ の分散は,
となる.この分散の平方根を回帰係数推定値 b^ の標準誤差という.
回帰係数の標準誤差による t 検定
目的変数 y が説明変数 x との回帰関係にないという
帰無仮説,
H0:b = 0,
を考えてみよう.
回帰係数 b の推定値 b^ の分散は,
と推定できるので,b^ の標準偏差(標準誤差)は, s b と推定
される.これより,回帰係数をその標準誤差で割った t 値が,帰無仮説のもとで,
のように,自由度 n−2 の t 分布に従うことを利用して回帰係数の検定が行える.すなわち,
自由度 n−2 の t 分布の 97.5%点を t0 とすると,
|t | > t0 → 帰無仮
説を有意水準 5 %で棄却(回帰関係が有意に認められる)
|t | ≦ t0
→ 帰無仮説を棄却しない(回帰関係が認められない)
と定式化できる.
分散分析
平方和分解
回帰式により,
従属変数 y のデータ yi は,
yi = y^i
+ (y^i −
yi ) =
回帰値 + 残差
のように分解される.この分解に対応して従属変数データの総平方和 ST は,
ST = Σi
(y i − y- )
2 =
Σi
(y^i − y- )
2 +
Σi
(y i −
y^i )
2 = SR + Se
総平方和 = 回帰平方和 + 残差平方和
のように分解される.これを平方和の分解という.この分解に対応して自由度は,
n−1 = 1 + n−2
と分解される.
決定係数(重相関係数の2乗)
データが直線回帰式でよく説明できるのは,回帰平方和が大きく,残差平方和
が小さい場合である.総平方和のうち回帰平方和で説明される割合を決定係数,もしくは
重相関係数の2乗といい,
で定義される.なお,重相関係数 R とは,データ y i
と回帰値 y^i との間の相関係数である.これより,
以下の分散分析表ができる.
回帰分析の分散分析表
| 変動因 | 平方和 | 自由度 | 平均平方 | F 値 |
| 回帰 | SR | 1 |
SR |
F = SR/se2 |
| 残差 | Se | n−2 |
se2 = Se/n−2 |
|
| 全体 | ST | n−1 |
|
|
F 検定
従属変数 y が説明変数 x の回帰関係にないという
帰無仮説,
H0:b = 0,
を考える.帰無仮説のもとでは,回帰平均平方 SR と残差分散 se2
がともに誤差 σ2 の不偏推定量になるので,
その比 F 値が,
F = SR/se2
〜 F(1,n−2),
という F 分布に従うことを利用して検定ができる.すなわち,分子,分母
自由度が 1,n−2 である F 分布 F(1,n−2)の95%点を F0 とすると,
F > F0 → 帰無仮説を有意水準 5 %で棄却(回帰関係が有意に認められる)
F ≦ F0 → 帰無仮説を棄却しない(回帰関係が認められない)
と定式化できる.
回帰係数に対する検定
前節では,H0:b = 0,の検定を考えたが,もっと一般の形の検定,
H0:b = b0,
も簡単に考えることができる.このときは,帰無仮説のもとで,
t = (b^ - b0)/s b 〜 t(n−2)
のように,自由度 n−2 の t 分布に従うことを利用して回帰係数の検定が行える.すなわち,
検定統計量として,この |t| 値を考えればよい.
回帰式の信頼区間
回帰係数の信頼区間
回帰係数の標準誤差 s b を用いて,
回帰係数 b の信頼区間がつくれる.すなわち,
自由度 n−2 の t 分布の 97.5%点を t0 とすると,
回帰係数 b の 95%信頼区間の幅 d は,d = t0
s b となるので, 95%信頼区間は,
b^ − t0
s b < b <
b^ + t0
s b
となる.
回帰直線の信頼区間
データから推定された回帰直線は,データの平均(x-,y-)
を通るので,
Y = y- + b^
(x - x-)
とおける.これより,Y の分散は,
となる.誤差分散 σ2 は,
データの残差分散 se2 で推定されるので,Y の標準誤差は,
となり,これが自由度 n - 2 を持つ.よって,推定回帰式にこの標準誤差の t0
倍を加えたものが,回帰式の 95%信頼幅となる.
回帰予測値の信頼幅
回帰式から得られる予測値 y~ は,回帰式に誤差項が加わって,
y~ = y- + b^
(x - x-)+ e
となるので,その分散は,
となる.先ほどと同様に,誤差標準偏差を残差標準偏差で置き換えると,回帰予測値 y~ の
標準誤差は,
となり,回帰式の 95%信頼幅の外側に回帰予測値の 95%信頼幅が描ける.
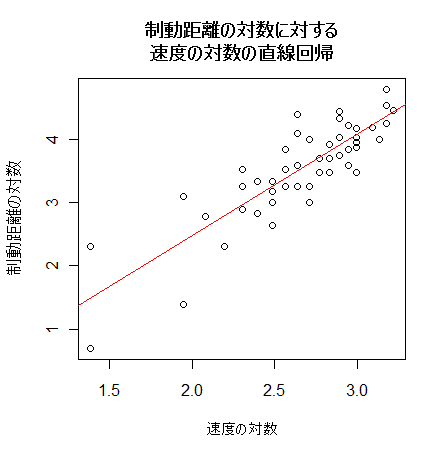
- 自動車の速度と制動距離の回帰係数に対する検定
物理法則によると,自動車の速度の2乗と制動距離が比例するので,求めた回帰係数は 2 となることが
期待される.このため,H0:b = 2,の検定を行ってみる.
これは,回帰係数の信頼区間を求め,これが 2 を含むかどうかでも調べることもできる.
bh <- summary(car.lm)$coefficient[2,1] # 回帰係数
sb <- summary(car.lm)$coefficient[2,2] # 回帰係数の標準誤差
tv <- abs(bh - 2)/sb; tv
edf <- summary(car.lm)$df[2] # 残差分散の自由度
2*(1 - pt(tv, df=edf)) # 有意確率
t0 <- qt(0.975, df=edf)
d <- t0*sb
bh - d # 95%信頼区間の下限
bh + d # 95%信頼区間の上限
new <- data.frame(x=seq(1.3, 3.5, by=0.02))
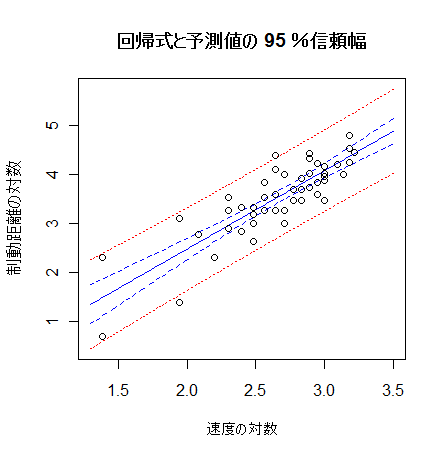
dc <- predict(car.lm, new, interval="confidence", level=0.95) # 回帰推定値(回帰直線)の 95 %信頼幅
dp <- predict(car.lm, new, interval="prediction", level=0.95) # 回帰予測値の 95 %信頼幅
matplot(new$x, cbind(dc,dp[,-1]), lty=c(1,2,2,3,3), type="l",
col=c("blue","blue","blue","red","red"), xlab="log of velocity", ylab="log of braking distance")
points(x, y)
|
ブートストラップ法による信頼区間の構成
回帰残差が正規分布するというモデルのもとでは,回帰係数推定量が t 分布に従う
ことを利用して,回帰係数の信頼区間を構成することができた.
回帰残差の正規性が疑われる場合や,正規性が成立しない場合
の信頼区間を構成する方法の一つとしてブートストラップがある.ブートストラップ法は,
大きさ n の標本(サンプル)から復元抽出
を許して新しく大きさ n の標本を生成する(リサンプリング)手法で,生成された標本ごとに回帰係数の
推定値が得られる.このブートストラップサンプルによる回帰式はサンプルごとに微妙に異なる.
1000回程度のリサンプリングを行えば,回帰係数が1000個得られるので,この分布から
回帰係数の信頼区間を構成することができる.
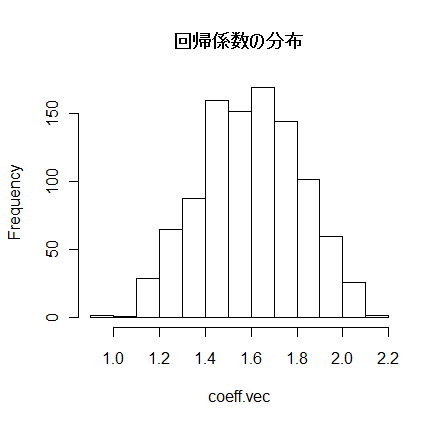
- 自動車の速度と制動距離の回帰係数における,ブートストラップによる信頼区間の構成
n <- length(y)
M <- 1000
coeff.vec <- NULL
for(i in 1:M){
nx <- sample(1:n, replace=TRUE)
bb <- (lm(y[nx] ~ x[nx]))$coefficients[2]
coeff.vec <- c(coeff.vec, bb)
}
hist(coeff.vec)
quantile(coeff.vec, c(0.025, 0.975)) # 95%信頼区間
|
ミヤマクワガタの相対成長解析
データダウンロード
成長段階の異なる 47 頭のミヤマクワガタのパーツ別の重量データ(g).パーツは,
頭部(WHEAD),前胸部(WTHORAX),中胸〜腹部(WABDOM),交尾器(WGENI)からなる.
形態形質 x,y に対して,初期成長指数を a,成長比を b と
したときの生物形態の相対成長式,
logy = loga + b logx
において,中胸〜腹部(WABDOM)の重量(g)を体サイズの指標 x としたとき,y として
頭部(WHEAD)の重量(g),前胸部(WTHORAX)の重量(g),交尾器(WGENI)の重量(g)
の3通りを考えたときの相対成長式の回帰係数をそれぞれ求める.
体の成長に合わせてパーツも比例して大きくなれば,成長比 b = 1 となるはずである.
- 問題1
-
- 帰無仮説 H0:b = 1
の検定を y を頭部,前胸部,交尾器としたときでそれぞれ行え.
- 回帰係数の 95%信頼区間をそれぞれ求めよ.
- 回帰係数の 95%信頼区間をブートストラップ法で求め,先ほどの信頼区間と比較せよ.
- 上記の結果から,ミヤマクワガタの相対成長に関して分かったことを考察せよ.
重回帰分析
統計モデル
説明変数が 2 つ以上になった場合である.いま,p 個の説明変数 x1,
x2,…,xp,により目的変数 y が,
y = b0 + b1x1 +
b2x2 + … + bpxm
+ e
と表現できるとする.ここで,b0b1,…,bp は
回帰係数,e は,誤差である.
ここで,n(n > p)個のデータがあり,目的変数が y
= (y1,…,yn)',j 番目の説明変数 xj の値が,
x1 = (x1j,…,xnj)' であったとする.
回帰係数ベクトルを b = (b0,…,bm)',誤差ベクトル
を e = (e1,…,en)' とすると,データが満たす構造
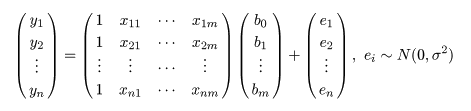
モデルは,
となる.ここで,誤差ベクトルは,平均 0,分散共分散行列 σ2I の n 次元
正規分布に従うとする.これは,n 個の誤差 ei が互いに独立に平均 0 分散 σ2
の正規分布に従うと考えたとき(普通行う仮定)の多変量表現である.
最小2乗法により,回帰係数の推定値は,
と求められる.
多変量の線形関数の平均と分散
p 変量確率変数 x の平均を μ,分散共分散行列を Σ とすると,任意の p×p スカラー
行列 A に対し,
E[Ax] = AE[x] = Aμ,
Var[Ax] = AVar[x]A' = AΣA',
が成り立つ.
回帰係数の分散
重回帰モデルの回帰係数ベクトルの推定量 b^ の分散は,
となる.残差分散 σ2 の推定値を se2 とすると,
回帰係数の分散は,se2(X'X)-1 で推定される.
ハット行列とてこ比
さて,回帰推定値ベクトル y^ は,
と書ける.ここで,H は,説明変数データベクトル y から
回帰推定値ベクトル y^ を生成する行列なので,ハット行列(hat matrix)と
呼ばれている.ハット行列の対角成分 hii が大きいと i 番目のデータは推定値に大きな
影響を及ぼすので,これを「てこ比(leverage)」と呼んでいる.てこ比の平均的な値は,(p + 1)/n なので,
たとえば,2(p + 1)/n より大きなてこ比をもつようなデータには注意を払う必要がある.すなわち,
このデータの存在が回帰係数の推定に大きな影響を与えているからである.
標準化残差
回帰残差推定量ベクトル e^ は,
とハット行列を用いて書ける.これより,その分散は,
となる.なお,I - H がべき等行列であることに注意せよ.従って,個々の
回帰残差推定量 e^i の分布は,
となる.この ri を標準化残差(standarized residual)と言う.
Cook 距離
個々のデータが回帰係数の推定値に与える影響を調べるため,i 番目のデータを除いたときの回帰係数
推定値を b^-i として,これが全データを用いたときの回帰係数
推定値 b^ との違いの大きさで測る.これが Cook 距離で,以下のように
定義される.
ここで,y^-i = Xb^-i で
ある.また,多少の計算により Cook 距離は標準化残差とてこ比で計算され,最後の式のように表せる.
Cook 距離が 0.5 を超えるとそのデータは影響が「大きい」とされ,1 を超えると影響が「特に大きい」と
される.
回帰診断
回帰分析を行ったときに,データが回帰モデルによくフィットしているかや,データの中に回帰モデル
からはずれたも(異常値)がないか,などを調べた方がより安全である.これを
回帰診断(regression diagnostics)という.
R などの統計ソフトが普及する以前は,手間がかかるので回帰診断まで行うことはあまりやらなかったが,
現在では手軽にできるので,行うのが普通になってきていると思われる.このため,回帰診断の考え方や
着目点などを理解する必要がでてきたと言える.
回帰診断は,以下の2点からなる.
- 誤差分析:回帰残差(誤差)は,独立,等分散,正規性の3つの仮定を置くことが普通であるが,これが
満たされているかを調べる.
誤差に何らかのトレンドが見られるときは回帰モデルがデータにフィットしていない
可能性があるので,別の回帰モデル(多項式回帰など)を試す必要がある.
極端に誤差の大きな観測値は異常値(out lier)の可能性がある.
- 感度分析:観測値(データ)が回帰係数に及ぼす影響をみる.少数のデータが回帰係数に大きな影響
を与えているときは,このデータの処遇を考える必要がある.
-
- 回帰診断の R スクリプト
-
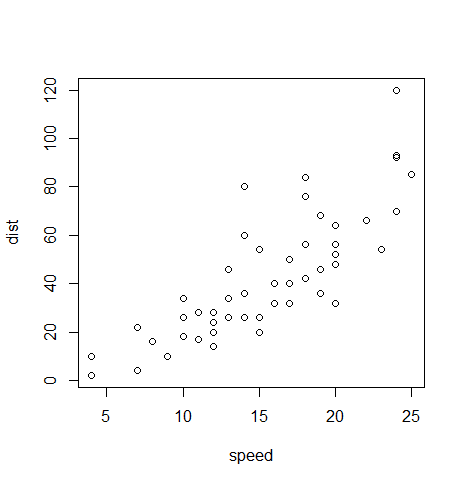
cars
plot(cars)
y <- log(cars$dist)
x <- log(cars$speed)
plot(x, y, xlab="log of velocity", ylab="log of braking distance")
car.lm <- lm(y ~ x)
abline(car.lm, col="red")
summary(car.lm)
plot(car.lm) # 回帰診断(たったこれだけ)
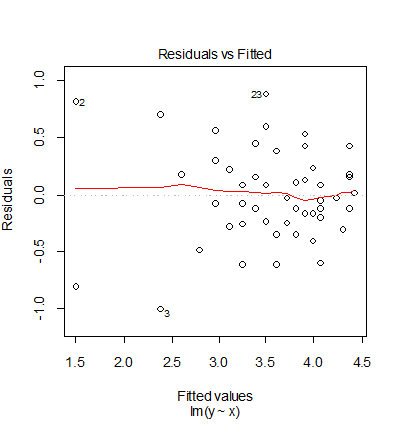
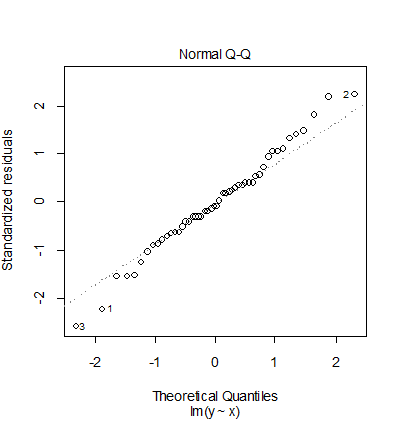
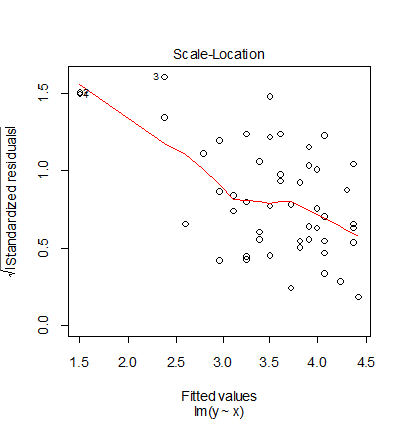
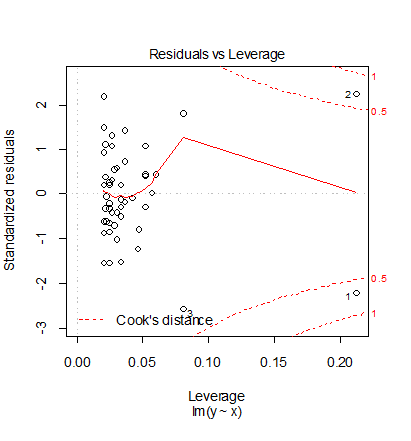
3番目の Scale-Location プロットで標準化残差の大きさが x が大きくなるにつれて小さくなる傾向
がありよくない.4番目の Residuals vs Leverage 1番と2番のレバレッジが大きく,Cook 距離も0.5を超えて
いて問題がある.これは,元データを対数変換したため,x の小さい方のデータ密度が減少した
ことによると考えられる.このため,このデータを対数変換して解析することは良くなく,元データに多項式
回帰をあてはめた方がよいと思われる.
 |
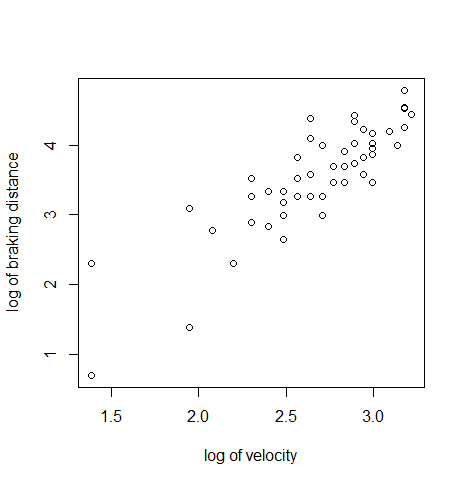 |
| もとデータ | 対数変換データ |
- 問題2
-
ミヤマクワガタの相対成長解析の回帰分析の回帰診断を行い,問題がないか考察せよ.
モデル選択と AIC
確率モデルのパラメータ推定には,通常,最尤法が用いられる.しかしながら,重回帰分析などで説明変数の
個数(パラメータ数)を決めようとすると,一般に,パラメータ数が多いほどデータへのモデルの当てはまり
(fitting)が良くなるので,最尤法でパラメータ数を決めるとパラメータ数の多いモデルが「良い」とされて
しまう.パラメータ数の多いモデルは,パラメータの値を推定したデータにはよく当てはまるが,
同様の状況から得られた別のデータへの当てはまりが悪くなることが知られている.このような現象を解釈
しすぎ(over fitting)という.
これを避けるには,できるだけ単純なモデルを考えるのがよいとされている.これを実現するモデル選択
の基準として,
X = (モデルのデータへの当てはまり) + (モデルの複雑さへのペナルティ)
の形式のものがいくつか提案されている.この中で有名な基準の一つが AIC (Akaike Information Criterion)
である.AIC は,
AIC = - 2×(モデルの最大対数尤度) + 2×(モデルの自由パラメータ数)
と定義される.モデルの最大対数尤度は,確率モデルの最尤推定値を確率モデルに代入したときの尤度の対数
を取ったものであり,モデルのデータへの当てはまりのよさを評価している.モデルの自由パラメータ数
は,モデルの複雑さの尺度の一つで,パラメータ数の少ないモデルほど単純でよいものと考えられる.
結局,AIC の小さなモデルがよいとされる.
k 個のパラメータ θ を持つ回帰モデル
y = f(x ; θ) + e
において,残差 e が正規分布に従うモデルでは,n 個のデータから得られた
残差分散の最尤推定値を v
2 とすると,
回帰モデルの最大対数尤度は,
l = -(1/2) [n log 2π + n log v2 + n ]
となる.これより,回帰モデルでの AIC は,
AIC = (n log 2π + n log v2 + n ) + 2k
となり,AIC の小さな回帰モデルがよいとされる.
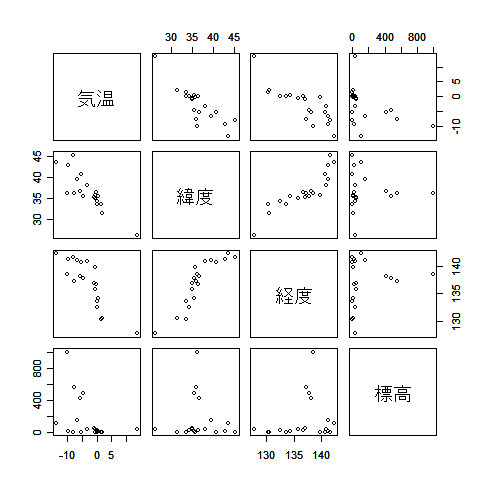
- 1 月の日最低気温の月平均値
1941年〜1970年での日本の各都市における 1 月の日最低気温の月平均値(y)が,各都市の緯度(x1),
経度(x2),標高(x3)でよく説明できるかを重回帰分析で解析してみる.データは以下の
通りである.
# 1 月最低気温重回帰の R スクリプト
|
kion <- read.csv("kion.csv")
| # 気温データ読み込み |
|
pairs(kion[,2:5])
| # 変数間散布図一覧 |
|
cor(kion[,2:5])
| # 変数間相関 |
|
kion1.lm <- lm(temp ~ lat + long + altitude, data=kion)
| # 3 変数重回帰 |
|
summary(kion1.lm)
| # 結果表示 |
|
anova(kion1.lm)
| # 分散分析表示 |
|
n <- nrow(kion)
| # データ数 |
|
x0 <- rep(1,n)
| # |
|
x <- as.matrix(cbind(x0, kion[,3:5]))
| # 説明変数行列 |
|
se2 <- anova(kion1.lm)[4,3]
| # 残差分散 |
|
v <- se2 * solve(t(x) %*% x)
| # 回帰係数の分散共分散行列 |
|
sqrt(diag(v))
| # 回帰係数の標準誤差 |
説明変数の選択
すべての組み合わせの AIC
全変数を使って重回帰分析を行ったが,経度(x
2)の回帰係数の有意確率が小さくないので,
経度の情報は気温を説明するのに必要ないかも知れない.これは日本では,緯度が高く標高が高いほど気温
が低いと考えられることとも一致している.モデル選択の方法として AIC を利用してみる.
3 個の説明変数があるので,説明変数の組み合わせは 2
3 = 8 通りある.このすべての組合わせ
に対して AIC の値を計算し,最も小さな値をもつモデルを採用することにする.
# 変数選択の R スクリプト
|
kion0.lm <- lm(temp ~ 1, data=kion)
| # 説明変数無し回帰 |
|
anova(kion0.lm)
| # |
|
kion11.lm <- lm(temp ~ lat, data=kion)
| # 説明変数:緯度,回帰 |
|
anova(kion11.lm)
| # |
|
kion12.lm <- lm(temp ~ long, data=kion)
| # 説明変数:経度,回帰 |
|
anova(kion12.lm)
| # |
|
kion13.lm <- lm(temp ~ altitude, data=kion)
| # 説明変数:標高,回帰 |
|
anova(kion13.lm)
| # |
|
kion21.lm <- lm(temp ~ lat + long, data=kion)
| # 説明変数:緯度,経度,回帰 |
|
anova(kion21.lm)
| # |
|
kion22.lm <- lm(temp ~ long + altitude, data=kion)
| # 説明変数:経度,標高,回帰 |
|
anova(kion22.lm)
| # |
|
kion23.lm <- lm(temp ~ lat + altitude, data=kion)
| # 説明変数:緯度,標高,回帰 |
|
anova(kion23.lm)
| # |
|
kion3.lm <- lm(temp ~ lat + long + altitude, data=kion)
| # 説明変数:緯度,経度,標高,回帰 |
|
anova(kion3.lm)
| # |
|
AIC(kion0.lm)
| # 説明変数無し回帰 AIC |
|
AIC(kion11.lm)
| # 説明変数:緯度,回帰 AIC |
|
AIC(kion12.lm)
| # 説明変数:経度,回帰 AIC |
|
AIC(kion13.lm)
| # 説明変数:標高,回帰 AIC |
|
AIC(kion21.lm)
| # 説明変数:緯度,経度,回帰 AIC |
|
AIC(kion22.lm)
| # 説明変数:経度,標高,回帰 AIC |
|
AIC(kion23.lm)
| # 説明変数:緯度,標高,回帰 AIC |
|
AIC(kion3.lm)
| # 説明変数:緯度,経度,標高,回帰 AIC |
変数増減法の AIC
説明変数の数が多くなり,すべての組み合わせを調べることが大変な場合には,変数増加法,変数減少法,
その組み合わせである変数増減法がある.ここでは,変数増減法もやってみる.
# 変数選択の R スクリプト
|
library(MASS)
| # MASS ライブラリィー読み込み |
|
null <- lm(temp ~ 1, kion)
| # 説明変数無し |
|
full <- lm(temp ~ lat + long + altitude, kion)
| # 説明変数3つ |
|
result <- stepAIC(null, scope=list(lower=null, upper=full), data=kion)
| # 変数増減法 |
|
summary(result)
| # 結果表示 |
- 問題3
-
AIC の値から気温を説明する最もよい回帰式を求めよ.
参考文献(古い順)
- Introduction to the Theory of Statistics, Mood, A. M., Graubill, F. A. & Boes, D. C., 1974,
McGRAW-HILL
- 「実験」生産環境生物学,東京大学大学院農学生命科学研究科生産・環境生物学専攻編,1999,朝倉書店
- 工学のためのデータサイエンス入門−フリーな統計環境Rを用いたデータ解析−,間瀬茂ら,2004,
数理工学社
- 実践生物統計学−分子から生態まで−(第 1 章,第 2 章),
東京大学生物測定学研究室編(大森宏ら),
2004,朝倉書店
- The R Tips データ解析環境 R の基本技・グラフィックス活用集,船尾暢男,2005,九天社
- R で学ぶデータマインニング I −データ解析の視点から−,熊谷悦生・船尾暢男,2007,九天社
- R で学ぶデータマインニング II −シミュレーションの視点から−,熊谷悦生・船尾暢男,2007,九天社
Copyright (C) 2008, Hiroshi Omori. 最終更新日:2014年10月27日