圃場実習

圃場実習データの解析

東京大学大学院農学生命科学研究科　大森宏

http://lbm.ab.a.u-tokyo.ac.jp/~omori/experiment12/zissyu2019.html

2019年12月18日

実習基本情報

2019耕種概要と品種

データ

2019年度: エクセルデータダウンロード(Alldata2019.xlsx)
Ｒ用データダウンロード(Rice2019.csv)

解析事例

収量の分散分析

　2019年度の水稲圃場実習では，要因として品種（4 品種）と施肥量（低窒素と高窒素）を取り上げた。施肥管理を効率的に行うため施肥管理を主区（1 次因子）、品種を副区（2 次因子）とした分割区法（split-plot design）を用い、3 反復の実験を行った。
　2019年度における試験区のある形質の測定値を X_ijk とすると， X_ijk の統計（構造）モデルは，a = 2，b = 4，r = 3，として，

X_ijk ＝ μ ＋ α_i ＋ ρ_k ＋ｅ¹_ik ＋ β_j ＋ (αβ)_ij ＋ｅ²_ijk， i ＝ 1，…，a，j ＝ 1，…，b，k ＝ 1，…，r

Σ_iα_i ＝ 0， Σ_jβ_j ＝ 0， Σ_i(αβ)_ij = Σ_j(αβ)_ij = 0，

とおける．ただし，μ は総平均，α_i は施肥効果，β_j は品種効果，(αβ)_ij は施肥量と品種の交互作用，ρ_k はブロック効果，ｅ¹_ijk は 1 次誤差、ｅ²_ijk は 2 次誤差である．ブロック効果は、 ρ_k ～ N(0，σ_B²）を満たす変量（確率変数）で、誤差は，ｅ¹_ijk ～ N(0，σ₁²）、ｅ²_ijk ～ N(0，σ₂²）を満たす互いに独立な変量であるとする．

　1 次誤差を用いて施肥効果やブロック効果を検定し、2 次誤差を用いて品種効果や施肥と品種の交互作用を検定する。このため乱隗法に比べ、 1 次因子（施肥量）の効果に対する精度は落ちるが、2 次因子（品種）や交互作用に対する精度は向上すると考えられる。

rice <- read.csv("Rice2019.csv")				# データ読み込み
dim(rice)
attach(rice)									# rice の使用宣言
y <- Grain_yield								# 収量を解析形質にする
Rep <- factor(Rep)
MainMean <- tapply(y, Main_plot, mean); MainMean
SubMean <- tapply(y, Subplot, mean); SubMean
RepMean <- tapply(y, Rep, mean); RepMean
GrandMean <- mean(y); GrandMean
x <- tapply(y, Subplot:Main_plot, mean); x
#   Calotoc:High_N     Calotoc:Low_N  Momiroman:High_N   Momiroman:Low_N 
#         353.1541          325.8600          311.4992          353.3201 
#    Teqing:High_N      Teqing:Low_N Yamadawara:High_N  Yamadawara:Low_N 
#         637.1483          548.0262          658.2531          666.3392 
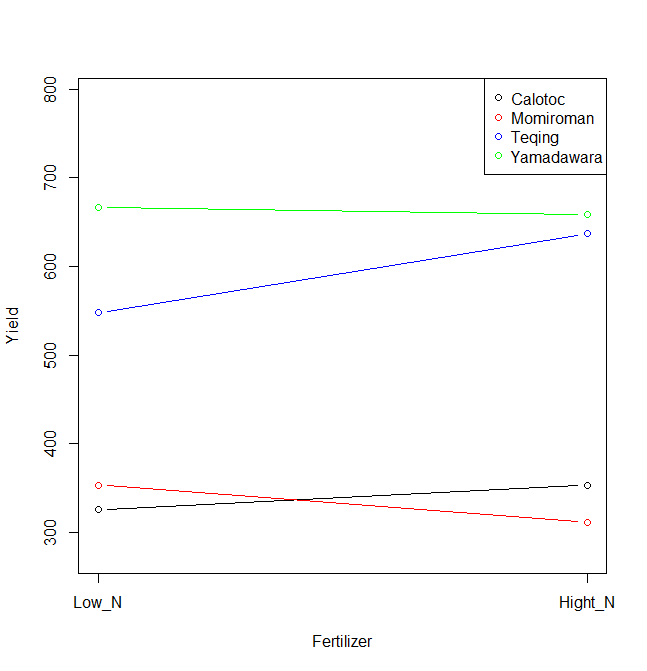
#収量のグラフ表示
plot(1:2, x[2:1], type="b", ylim=range(y), xaxt="n", xlab="Fertilizer", ylab="Yield")
axis(1, 1:2, labels = c("Low_N", "Hight_N"))
points(1:2, x[4:3], type="b", col="red")
points(1:2, x[6:5], type="b", col="blue")
points(1:2, x[8:7], type="b", col="green")
legend("topright", legend=c("Calotoc","Momiroman","Teqing","Yamadawara"),
pch=1, col=c("black","red","blue","green"))
# 分割区法分散分析
summary(aov(y ~ Main_plot*Subplot + Error(Rep/Main_plot)))
#
# 平方和分解の詳細
a = 2; b = 4; r = 3
# 1 次因子
RepEffect <- RepMean - GrandMean
RepV <- RepEffect[Rep]
RepSS <- sum(RepV^2); RepSS					# 12390：ブロック平方和
RepMS <- RepSS/(r - 1); RepMS				# 6195：ブロック平均平方
MainEffect <- MainMean - GrandMean
MainV <- MainEffect[Main_plot] 
MainSS <- sum(MainV^2); MainSS				# 1658.804：1 次因子平方和
MainMS <- MainSS/(a - 1); MainMS			# 1658.804：1 次因子平均平方
MainRepMean <- tapply(y, Main_plot:Rep, mean); MainRepMean
MM3 <- rep(MainMean, each=3)
RM2 <- rep(RepMean, 2)
GM6 <- rep(GrandMean, 6)
MainRepEffect <- MainRepMean - MM3 - RM2 + GM6; MainRepEffect
Error1V <- MainRepEffect[Main_plot:Rep]
Err1SS <- sum(Error1V^2); Err1SS 			# 3920.167：1 次誤差平方和
Err1MS <- Err1SS/((a -1)*(r - 1)); Err1MS	# 1960.084：1次誤差平均平方
RepF <- RepMS/Err1MS; RepF					# 3.16058：ブロック F 値
RepP <- 1 - pf(RepF, r-1, (a -1)*(r - 1)); RepP		# 0.2403511：ブロック p 値
MainF <- MainMS/Err1MS; MainF						# 0.8462927：1 次因子 F 値
MainP <- 1 - pf(MainF, a-1, (a -1)*(r - 1)); MainP	# 0.4547188：1 次因子 p 値
# 2 次因子
SubEffect <- SubMean - GrandMean
SubV <- SubEffect[Subplot]
SubSS <- sum(SubV^2); SubSS					# 524504.3：2 次因子平方和
SubMS <- SubSS/(b - 1); SubMS				# 174834.8：2 次因子平均平方
MainSubMean <- tapply(y, Main_plot:Subplot, mean); MainSubMean
MM4 <- rep(MainMean, each=4); MM4
SM2 <- rep(SubMean, 2); SM2
GM8 <- rep(GrandMean, 8); GM8
MainSubEffect <- MainSubMean - MM4 - SM2 + GM8; MainSubEffect
MainSubV <- MainSubEffect[Main_plot:Subplot]
MainSubSS <- sum(MainSubV^2); MainSubSS				# 14094.34：交互作用平方和
MainSubMS <- MainSubSS/((a - 1)*(b - 1)); MainSubMS	# 4698.114：交互作用平均平方
GMV <- rep(GrandMean, length(y))
Error2V <- y - GMV - RepV - MainV - Error1V - SubV -MainSubV
Err2SS <- sum(Error2V^2); Err2SS 			# 35846.14：2 次誤差平方和
Err2MS <- Err2SS/(a*(b - 1)*(r - 1)); Err2MS		# 2987.179：2 次誤差平均平方
SubF <- SubMS/Err2MS; SubF					# 58.5284：2 次因子F値
SubP <- 1 - pf(SubF, b - 1, a*(b - 1)*(r - 1)); SubP	# 1.953899e-07：2 次因子 p 値
MainSubF <- MainSubMS/Err2MS; MainSubF					# 1.57276：交互作用 F 値
MainSubP <- 1 - pf(MainSubF, (a - 1)*(b - 1), a*(b - 1)*(r - 1)); MainSubP	# 0.2472641：交互作用 p 値

収量の分散分析の結果

#結果
Error: Rep
          Df Sum Sq Mean Sq F value Pr(>F)
Residuals  2  12390    6195               

Error: Rep:Main_plot
          Df Sum Sq Mean Sq F value Pr(>F)
Main_plot  1   1659    1659   0.846  0.455
Residuals  2   3920    1960               

Error: Within
                  Df Sum Sq Mean Sq F value   Pr(>F)    
Subplot            3 524504  174835  58.528 1.95e-07 ***
Main_plot:Subplot  3  14094    4698   1.573    0.247    
Residuals         12  35846    2987                     
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1

収量の分散分析表

要因	自由度	平方和	平均平方	F 値	p 値
ブロック	2	12390	6195	3.161	0.240
1 次因子（施肥量）	1	1659	1659	0.846	0.455
1 次誤差	2	3920	1960
2 次因子（品種）	3	524504	174835	58.528	0	***
施肥量×品種	3	14094	4698	1.573	0.247
2 次誤差	12	35846	2987

　施肥効果は全体的に無く、品種による収量の違いが大きく認められた。また、交互作用も認められなかった。

参考：乱塊法

　4月17日に行った圃場試験実習の第 1 回、試験区の設計・設定の講義の中で、実験計画における最も重要な原則として、 Fisher の 3 原則を確認した。これは、

反復（繰り返し）
無作為化
局所管理（ブロックの作成）

からなる。Fisher の 3 原則に忠実な試験配置が乱塊法（randomized block design）である。今回の試験実習を乱塊法で行うとすると、施肥管理と品種組合せをブロック内で無作為に配置しなければばらない。最初に述べたように、施肥管理を効率的に行うため、乱塊法ではなく分割区法による実験を行った。
　前節では、分割区法における分散分析の結果を述べたが、この実験がもし乱塊法で行われていた場合どのような結果になるかみてみよう。試験区のある形質の測定値を X_ijk とすると、 X_ijk の乱塊法における統計（構造）モデルは， a = 2，b = 4，r = 3，として，

X_ijk ＝ μ ＋ α_i ＋ β_j ＋ (αβ)_ij ＋ ρ_k ＋ｅ_ijk， i ＝ 1，…，a，j ＝ 1，…，b，k ＝ 1，…，r

Σ_iα_i ＝ 0， Σ_jβ_j ＝ 0， Σ_i(αβ)_ij = Σ_j(αβ)_ij = 0，

とおける。ただし，μ は総平均，α_i は施肥効果，β_j は品種効果，(αβ)_ij は施肥量と品種の交互作用，ρ_k はブロック効果，ｅ_ijk は誤差である．ブロック効果は、 ρ_k ～ N(0，σ_B²）を満たす変量（確率変数）で、誤差は，ｅ_ijk ～ N(0，σ²）を満たす互いに独立な変量であるとする．

# 乱塊法分散分析
summary(aov(y ~ Main_plot*Subplot + Rep))

乱塊法としたときの収量の分散分析表

要因	自由度	平方和	平均平方	F 値	p 値
ブロック	2	12390	6195	2.181	0.150
施肥量	1	1659	1659	0.584	0.457
品種	3	524504	174835	61.552	0	***
施肥量×品種	3	14094	4698	1.654	0.222
誤差	14	39766	2840

　分割区法と乱塊法での計算上の違いは、誤差平方和の違いだけである。乱塊法における自由度 14 の誤差平方和 39,766 が、分割区法では自由度 2 の 1 次誤差 3,920 と自由度 12 の 2 次誤差35,846に分解（3920 + 35846 = 39766）される。今回は 1 次誤差がそれほど大きくなかったので 2 次誤差はそれほど小さくならなかった。場合により、 1 次誤差が大きくなったときは 2 次誤差が小さくなるので、このときは乱塊法より分割区法の方が交互作用の検出力が増す可能性がある。

最終更新：2019年12月17日