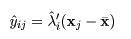| 主成分分析による評価次元の抽出
(SD法による庭景観写真の評価) |
対象が p 個の連続型変量 x =
(x1,…,xp)' で計測
されていて,その分散共分散行列が Σ であるとする.
このとき,変量の線形結合,
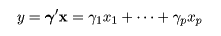 で表現される主成分 y を用いて,
変量全体のもつ変動 Σ をなるべく少数の次元(2,3次元)
で記述しようとする手法が主成分分析(principle component analysis)である.
これにより,対象のちらばりが散布図で視覚化され,対象全体の構造が見て取れる.
で表現される主成分 y を用いて,
変量全体のもつ変動 Σ をなるべく少数の次元(2,3次元)
で記述しようとする手法が主成分分析(principle component analysis)である.
これにより,対象のちらばりが散布図で視覚化され,対象全体の構造が見て取れる.
主成分の固有値と累積寄与率
| 主成分 |
第1 |
第2 |
第3 |
第4 |
第5 |
| 固有値 |
4.353 |
2.807 |
1.003 |
0.479 |
0.165 |
| 累積寄与率 |
0.484 |
0.795 |
0.907 |
0.960 |
0.978 |
主成分分析では,抽出された成分の変動の大きさが固有値で得られる.
抽出した次元までで説明される変動の割合を示すのが累積寄与率である.
上にこれらの値が示されている.これをみると,第2主成分までで全変動
の 80% 近く,第3主成分までで 90% 以上の変動が説明できるので,
元々の9個の評価項目は2次元で十分説明可能であり,3次元までとればほぼ
完全に説明できることがわかる.
また,第1,第2,第3主成分に対する係数(
固有ベクトル
)や元の変数に対する相関を表す
因子負荷量(factor loading)
をみると,各主成分にどの変数が関与しているかがわかる.
主成分分析による庭景観写真付置
(第1−第2主成分得点散布図)

|
第1主成分は,
「1:好き」,「7:整然」,「9:広々」などの評価尺度と比較的大きな正の
相関があり,「2:住みたくない」,「6:ストレス」などの評価尺度と比較的大きな負の相関をもつので,
「居住空間としての望ましさ」という「価値」
を表現していると考えられる.つまり,第1主成分の
大きな対象(左図の右側)は,
「広々として整然としているのは好ましく,くつろげるので住みたい」
庭景観となる.
一方,第2主成分は,「4:退屈」,「8:緑少ない」,「7:整然」
などの評価尺度と比較的大きな正の相関があり,
「5:複雑」という評価尺度と比較的大きな負の相関をもつので,
「鑑賞用途としての庭景観」という「趣味」を表していると考えられる.
すなわち,第2成分の負の絶対値が大きな対象(左図の下側)は,
「緑が多く,複雑で雑然としているのは面白い」
庭景観であると考えられる.
第3主成分は「3:なじみがある」と突出した正の相関があり,第1,第2主成分で説明されなかった
「3:なじみ」,すなわち,「いかにもありそうな庭景観」という
「標準」を表現する成分であることがわかる.
主成分分析
- 主成分の導出
p 次元確率変数ベクトル x の任意の線形結合
y = γ'x の中で,その分散が最大になるものを求めたい.
であるから,γ'γ = 1 という制約を設けると,ラグランジュの
未定係数法により求められる.つまり,
を γ で偏微分して 0 とおけばよい.これより,
という Σ の固有値問題になり,固有値 λ がy の分散となる.
Σ は実対称行列なので,その階数が p であるならば p 個の
正固有値があり,
対応する固有ベクトルは互いに直交する.これより,固有値を大きさの順に
λ1,λ2,… と取り出す.固有値 λi に
対応する固有ベクトル γi =
(γi1,…,γip)' が
生成する変量 yi = γi'x を
第 i 主成分と言う.
- 寄与率
λ1+ … +λp = trΣ であるから,
qi = λi/trΣ を第i 主成分の寄与率といい,
q1+ … +qi を第i 主成分
までの累積寄与率という.
- 因子負荷量
固有ベクトルでつくる直交行列を Γ =
(γ1…γp) とすると,
主成分の組 y = (y1,…,yp)' は
直交変換 y = Γ'x でつくられる.すると,固有値からなる
対角行列 Λ = diag(λ1,…,λp) を用いて,
となる.これより,主成分 yi ともとの
変数 xj との相関は,
となる.これを因子負荷量(factor loading)という.
- スペクトル分解
Σ は,直交行列 Γ と対角行列 Λ により,
と表現できる.これをスペクトル分解と言う.
いま,r (<p) 次元まででのスペクトル分解の和を,
とすると,Σr は Σ をr 次元で近似したもの
とみなせる.この近似は,tr((Σ - Σr)2)
を最小化したものになっている.
主成分の推定
平均 μ 分散共分散行列 Σ をもつ p 次元母集団から
大きさ n の無作為標本 x1,…,
xn がを抽出されたとする.μ は標本平均
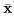 ,
Σ は標本分散共分散行列 S で推定される.
主成分分析は S もしくは,標本相関行列 R の
固有値を求めて行う.標本より得られた固有値と固有ベクトル
を本来の固有値と固有ベクトルの推定値とする.
,
Σ は標本分散共分散行列 S で推定される.
主成分分析は S もしくは,標本相関行列 R の
固有値を求めて行う.標本より得られた固有値と固有ベクトル
を本来の固有値と固有ベクトルの推定値とする.
第 i 主成分の標本値を主成分スコアという.j 番目の標本の
主成分スコアは,
となり,第1主成分と第2主成分による標本の主成分スコアの散布図を
眺めて標本のちらばり具合を調べる.
最終更新日:2004年 5月20日
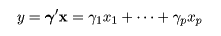
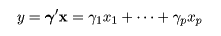

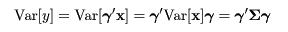
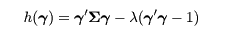
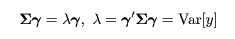
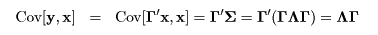
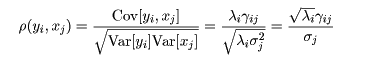
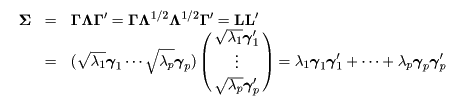
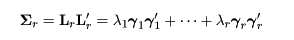
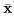 ,
Σ は標本分散共分散行列 S で推定される.
主成分分析は S もしくは,標本相関行列 R の
固有値を求めて行う.標本より得られた固有値と固有ベクトル
を本来の固有値と固有ベクトルの推定値とする.
,
Σ は標本分散共分散行列 S で推定される.
主成分分析は S もしくは,標本相関行列 R の
固有値を求めて行う.標本より得られた固有値と固有ベクトル
を本来の固有値と固有ベクトルの推定値とする.