多くの変量の背後にある比較的少数の観測されない因子（潜在因子） で，変量間の共分散や相関構造をモデル化するのが因子分析 (factor analysis)で， おもに心理学的な測定に対してもちいられてきた． 最近では，より幅広い構造モデルを解析する共分散構造解析の基本モデルの一つ という位置づけにある．
　通常，潜在因子は元の変量の線形結合で表現し，その係数を因子負荷量という． 評価尺度変量が多変量正規分布に従うと仮定すると， 因子負荷量を未知母数（パラメータ）として分散共分散行列（相関行列）が構造化される． 最尤法(maximum likelihood)により，データに最も適合する母数の値が推定され， これにより潜在因子が同定される．
　因子分析から推定される因子負荷量には直交回転の自由度があり，一意的には決まらない． そこで，各因子の負荷量にできるだけ「めりはり」をつけたバリマックス(varimax)解 で因子の解釈を行う．この解でも因子の解釈に不満がある場合は，斜交回転も許す プロマックス(promax)解を求める．

　主成分分析の結果から，第2もしくは第3主成分までで変動が説明できるので， 2つ，もしくは3つの潜在因子を仮定した因子モデルを考慮対象とする． 因子の係数である 因子負荷量 をみると，バリマックス解とプロマックス解はほとんど同じであった．
　2因子モデルでの因子の解釈は，第1因子が，「1：好き」，「2：住みたくない」，「6：ストレス」，「7：整然」， 「9：広々」といった評価尺度で構成される因子で，「居住性因子」と解釈できる． 一方，第2因子は，「4：退屈」，「5:複雑」，「7：整然」，「8:緑少ない」という評価尺度 で構成される因子で，「鑑賞因子」と解釈でき，主成分での解釈とほぼ同様であった．

因子分析

• 直交因子モデル
  p 次元確率変数ベクトル x = (x₁,…,x_p)' の平均が μ，分散共分散行列が Σ であるとする． 因子分析モデルは，観測できる変量 x の背後に少数の潜在変量 （共通因子）f = (f₁,…,f_m)'， m ＜p を仮定する． これらは，平均 0，分散 1 で互いに独立であるとする．
  また，共通因子で説明できない部分を誤差，もしくは，特定因子といい， e = (e₁,…,e_p)' と表す． すると，観測変量は，
  
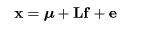
  とモデル化される．ここで，p ×m 行列 L = (l_ij ) は因子負荷行列 と呼ばれ，要素 l_ij は，i 番目の 変数の j 番目の因子への負荷を与える．
  　
• 分散共分散行列の構造化
  直交因子モデルのもとでの観測変量 x の分散共分散行列は，
  
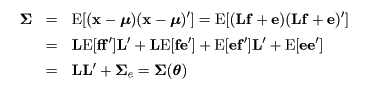
  と構造化され，推定すべきパラメータは，
  
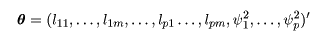
  となる． これより，変量 x_i の分散は，
  
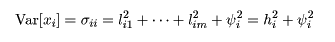
  と分解される．h_i²/σ_ii を 共通度といい，ψ_i² を特定分散という．
  　
• 因子負荷の不確定性
  ところで，T を m ×m のある直交行列とし， L^* = LT，f^* = fT とした因子負荷行列と潜在因子を考えてみると，
  
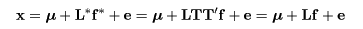
  となり，もとのモデルと区別がつかず，分散共分散行列の構造化も同一になる． つまり，因子モデルは直交変換での不定性がある．これより，解釈のしやすいように 因子回転を行っても問題はない．
  　
• 最尤推定
  平均 μ 分散共分散行列 Σ(θ) をもつ p 次元 正規母集団から 大きさ n の無作為標本 x₁，…， x_n がを抽出されたとする．対数尤度は，
  
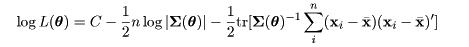
  となる．これを最大にするようなパラメータ θ を適当なアルゴリズム で数値的に求める．
  　
• バリマックス回転
  最尤法による因子負荷行列の推定値は，解の一意性を満たすために， LΣ_e^-1L が対角行列という制約条件 を課している．この条件下での因子負荷量は解釈のしやすさとは関係しない． 解釈のしやすい負荷とは， 各変量が１つの因子に高い負荷を与え，残りの因子には低い負荷を与えるようになっている 場合である．これを行うのによく用いられているのがバリマックス回転である．
  いま，上記の制約条件下で得られた因子負荷行列の推定値 L に適当な 直交変換 T をほどこし， L^* = (l_ij^* ) = LT を 新しい因子負荷行列にしたとする．このとき，
  
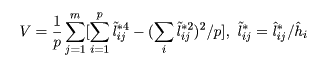
  を最大にするような直交変換 T を求める．