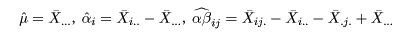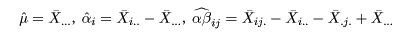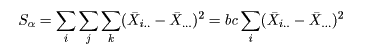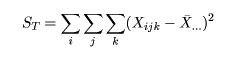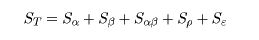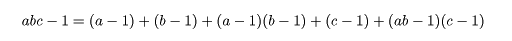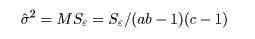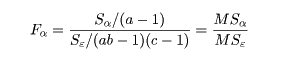| 施肥量の効果は本当か
(どの効果があるのか:分散分析と F 検定) |
構造モデル
処理組み合わせでラベルをつけた収量値 Xijk は,処理効果により,
Xijk = μ + αi + βj + ρk
+ (αβ)ij + εijk, i = 1,2, j = 1,2,3, k = 1,2
と構造化(モデル化)できる.ここで,μ は総平均で
αi は栽植密度の
主効果(main effect)であり,βj は施肥量主効果,
ρk はブロック効果,(αβ)ij は栽植密度と施肥量の交互作用(interaction)で,
各効果の和は0,たとえば,Σ αi = 0,とする.
また,εijk はこれらの効果で説明できない誤差で,
互いに独立に
平均 0,分散 σ2 の正規分布(normal distribution)
に従う (εijk 〜 N(0, σ2)) と仮定する.
各効果の推定値は,たとえば,
と表せる.
処理平方和
効果の大きい処理に対しては各効果の水準ごとの推定値は大きく異なり,逆に各水準
ごとに同じような値の推定値を与えるような処理は効果が小さいと考えられる.
これは処理平方和(sum of squares; SS)で測ることができる.
たとえば,密度の主効果の平方和は,
である.実は,
データがもつ全平方和(sum of squares; SS)
は,以下に示すように各処理による平方和で分解され,
となる.これと同様に,各処理平方和に対する自由度(degree of freedom)も
となる.なお自由度とは,比較の数のことで,3水準の試験では比較は2通り
(水準1対水準2,水準2対水準3)なので自由度は2となる.
また,比較1つ分の平方和が平均平方(mean squares; MS)で,
平方和を自由度で割った値である.たとえば,密度効果の平均平方は,
MSα = Sα/(a-1) である.
また,誤差分散は,
のように誤差平均平方で推定する.各効果の大きさは,この
誤差の大きさと比較することにより測ることができる.
F 検定
各処理にまったく効果がないという帰無仮説(null hypothesis),つまり,
H0 : αi = 0, βj = 0
という条件のもとで各処理効果の平均平方を誤差平均平方で割った値が F 分布に従う
ことにより各処理効果の検定(test)が行える.たとえば,密度主効果の検定は,
を用いる.密度効果がなければ Fα は 1 に近い値をとる.大きな
値を取った場合は,密度効果がないという帰無仮説が成立しておらず,
密度効果が認められると考える.つまり,帰無仮説を棄却(reject)する.
この大きさの基準として,慣習的に F 分布(自由度 a - 1, (ab - 1)(c - 1) )の
5 % や 1 % 点が用いられている.この基準確率を
有意水準(significance level)という.
収量に対する処理効果の分散分析表
| 要因 | 自由度 | 平方和 | 平均平方 |
F 値 | p 値 |
| ブロック | 1 | 15862 |
15862 | 3.85 | 0.107 |
| 密度 | 1 | 1419 |
1419 | 0.348 | 0.583 |
| 施肥 | 2 | 65029 |
32514 | 7.898 | 0.028 | * |
| 密度×施肥 | 2 | 2222 |
1111 | 0.270 | 0.774 |
| 誤差 | 5 | 20583 |
4117 | | |
|
| * : 5 % 有意 |
分散分析
各処理の効果の程度を
まとめたのが分散分析(analysis of variance; ANOVA)
であり,その結果は上の表にまとめられている.
これをみると,施肥量の効果の平方和は3水準で Sβ=65029 となり,比較は2通り
なので自由度は2となる.その平均平方は平方和を2で割り,MSβ=32514 である.
この値と誤差平方和の比が F 値で,7.90と大きな値になった.
帰無仮説のもとで F 値より大きな値がでる確率が p 値(p - value)である.p 値が小さいことは,
帰無仮説が成立する可能性が小さい,つまり,
処理効果が存在する可能性が大きいことを意味する.
この例では,統計的にみて
有意水準 3 % で施肥量により収量が異なるといえるが,他の処理
効果は認められなかったという結論になる.つまり,平均値から得た類推は,
統計的に根拠があったということになる.
2000年度収量データ分散分析
ry.aov <- aov(yield0 ~ blk0 + dens0 + fert0 + dens0:fert0)
summary(ry.aov)
#分散分析表の表示
blk0 などは主効果であり,dens0:fert0 は
交互作用である.yield0 は標本データを辞書式に並べたベクトルに対応し,
blk0 + dens0 + fert0 + dens0:fert0 の部分は処理水準ラベルにより計画行列
を生成させることに対応している.
最終更新日:2004年 5月20日