収量構成要素である「単位面積あたりの穂数(sn)」，「一穂籾数(gn)」， 「登熟歩合(pr)」， 「玄米千粒重(gw)」という順の4変量での処理効果をみるため，多変量分散分析を行った． 後の解釈を容易にするため，各変量平均0，分散1 に標準化した．
　Wilks の Λ による処理効果の分散分析は下の表である． これをみると，主効果はいずれも有意であった．注目すべきは，栽植密度と施肥量 の交互作用が有意となったことである．収量では栽植密度による効果は交互作用． 主効果ともに認められなかったが，収量構成要素では栽植密度効果が認められた． 他の検定統計量でも同様な結果が得られた．

栽植密度と施肥量の交互作用(穂数と千粒重)

　栽植密度と施肥量の交互作用は，どのように表れたかを詳しくみてみよう． 栽植密度と施肥量の交互作用仮説行列を H_αβ とする．自由度 が 2 なので，H_αβE^-1 の固有値は 2 個得られる． 最大固有値を λ_αβ とし，固有ベクトルを v_αβ とする． λ_αβ = 0.563 で，全体の 62.4% を説明していた．また， v_αβ = (-0.4697, -0.0684, 0.0791, 0.8766)' となった．
　固有ベクトルの値が各変量に対する寄与を表すので，この交互作用は， 1 番目の「穂数」と 4 番目の「千粒重」とで構成されている ことがわかる．標準化したデータで，この2つの変量の交互作用の様子を示したグラフが右 図である．これをみると，「穂数」は，疎植(density1)のときは多 肥(fert3)にすると大きく増加するが，密植(density2)のときはそれ程増加しない． 一方，「千粒重」は，密植(density2)で少肥のとき大きく減少している． これらが交互作用として現れたことがわかる．

R のコマンド

• 多変量分散分析
  Yrice.mat <- as.matrix(scale(rice.dfr[,7:10]))
  rice.ma <- manova(Yrice.mat ~ dens + fert + year +
       dens:fert + fert:year + dens:year + dens:fert:year)
  summary.aov(rice.ma)      #変量ごとの分散分析
  rice.ma.sum <- summary(rice.ma, test="Wilks")
  rice.ma.sum
  5 〜 8列目の収量構成要素の4変量で多変量分散分析を行う． scale() を用いて各変量を平均 0，分散 1 に標準化する．検定統計量はデータの相似変換に対して不変である． Yrice.mat がデータ行列に対応し， dense + fert + year + dens:fert + fert:year + dens:year + dens:fert:year の部分が計画行列生成の項で，先ほど の4年次の分析の設定と同じである． 検定にはWilks の Λ を用いた．
• 栽植密度と施肥量の交互作用
  dfint.mat <- rice.ma.sum$SS$"dens:fert"
  error.mat <- rice.ma.sum$SS$Residuals
  dfint.eig <- eigen(dfint.mat %*% solve(e2.mat))
  dfint.eig
  s <- sum(dfint.eig$values)
  cumsum(dfint.eig$values/s)
  栽植密度と施肥量の交互作用偏差積和行列 H_αβ を dfint.mat で取り出し， 誤差偏差積和行列 E を error.mat で取り出し, H_αβE^-1 の固有値を eigen() で求める．
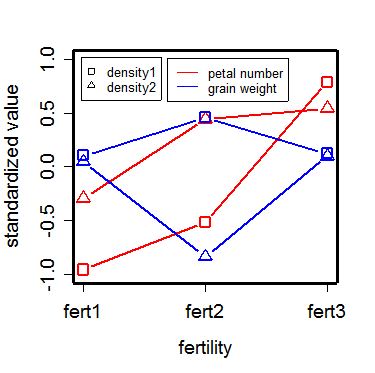
• グラフ表示
  pn1 <- tapply(Yrice.mat[,1], dens:fert, mean)
  gw1 <- tapply(Yrice.mat[,4], dens:fert, mean)
  x <- pn1
  plot(1:3, x[1:3], type="b", lwd=2, cex=1.5, xaxt="n",
       xlab="fertility", ylab="standardized value",ylim=c(-1,1), pch=0,cex.lab=1.2,cex.axis=1.2, col="red")
  axis(1, 1:3, labels=c("fert1","fert2","fert3"),cex.axis=1.2)
  box(lwd=3)
  par(new=T)
  plot(1:3, x[4:6], type="b",lwd=2, cex=1.5,
       axes=F, xlab="", ylab="" ,ylim=c(-1,1), pch=2, col="red")
  x <- gw1
  par(new=T)
  plot(1:3, x[1:3], type="b", lwd=2, cex=1.5,
       axes=F, xlab="", ylab="",ylim=c(-1,1), pch=0,col="blue")
  par(new=T)
  plot(1:3, x[4:6], type="b",lwd=2, cex=1.5,
       axes=F, xlab="", ylab="" ,ylim=c(-1,1), pch=2,col="blue")
  legend(locator(1),legend=c("density1","density2"),pch=c(0,2),cex=0.8)
  legend(locator(1),legend=c("petal number","grain weight"),
       lty=c(1,1), col=c("red","blue"),cex=0.8)