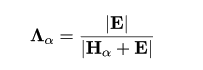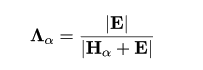| 多変量分散分析モデル
(他の形質の変動はどうか:多変量分散分析) |
形質 h の 4 年次にわたるデータは,先ほどの収量データと同様に,
Xhijkl = μh + αhi
+ βhj + γhk
+ (αβ)hij + (βγ)hjk + (αγ)hik
+ (αβγ)hijk + εhijkl
と書ける.αhi が密度効果,
βhj が施肥量効果,γhk が年次効果,
εhijkl が誤差である.ここで,
εijkl = (ε1ijkl, …, εpijkl)' を
誤差ベクトルとすると,これは互いに独立に,
εijkl 〜 N(0, Σε),つまり,
平均 0,分散共分散行列 Σε の
多変量正規分布(multivariate normal distribution)に従うことを仮定する.
1 変量分散分析では,形質 h に対して平方和が各処理ごとに
ShT = Shα + Shβ
+ Shγ + Shαβ + … + Shε
と分解され,各処理効果はおのおのの自由度でわった平均平方を誤差平均平方(MShε)
で割った F 値を検定統計量とした.たとえば,栽植密度効果(α)の検定では,
Fα = MShα /MShε
を用い,F 検定を行った.
多変量分散分析のモデルは,p 変量の偏差積和行列 T が各処理ごとに,
T = Hα + Hβ + Hγ
+ Hαβ + … + E
と分解される.H を仮説行列,E を誤差行列という.
仮説行列や誤差行列の対角成分には各変量ごとの平方和の値が入り,非対角成分には
変量の組の共分散の値が入る.つまり,変量間の相関が各処理効果ごとに分解される.
各処理効果に対する検定統計量はいくつかのものがある.
いま,栽植密度効果 (Hα) の検定を考えると,
よく知られているのが,尤度比から得られる Wilks の Λ,
である.また,Roy の HαE-1 の最大固有値も
よく用いられている.
最終更新日:2004年 5月20日