非負のn ×m データ行列 F = (fij ) に対し, n ≧m を仮定するが, そうでないときは,以下の算法でn とm を逆にして行う.
要素総和を f.. = ΣΣfij,行和列和をそれぞれ, f.j = Σifij, fi. = Σjfij とし, これらを対角要素とする行列をそれぞれ, C = diag(f.1,…,f.m), R = diag(f1.,…,fn.) とする.
このとき,対象座標 x = (x1,…,xn)' と カテゴリー座標 y = (y1,…,ym)' 間の 性格づけデータによる重み付け距離
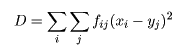
を最小にするような座標 x,y を求める ことにより両者の対応づけを行う.
この数量は相対的なもの(間隔尺度)なので, 一意的に決定するために対象とカテゴリー座標の重みつき 平均と平方和を標準化する. 対象座標では,
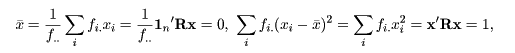
を仮定する.カテゴリ−座標でも同様である.
標準化した座標系では,重み付け距離は
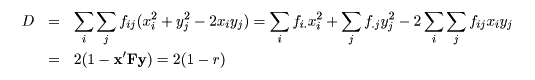
となる.ただし,r は対象数量とカテゴリー数量間の相関,
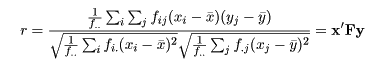
である.つまり, 重み付け距離 D の最小化は相関 r を最大にすることと一致する.
相関の最大化は,ラグランジュ(Lagrange)の未定係数法を用いて,
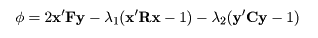
を x,y で偏微分して0とおけばよい. これより,連立方程式
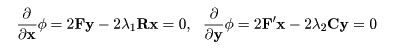
が得られる.
連立方程式にそれぞれ x,y を左から かけると,r = x'Fy =λ1 =λ2 が得られる. これより,x = R-1Fy/r となるので代入 して整理すると,
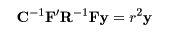
という固有値問題になる.最大固有値は1なので,第2固有値以降を 大きさの順に取り出す.固有値が相関の2乗で, 固有ベクトル y がカテゴリー座標になる.対象座標 x は y から 求められる.
なおこの固有値問題は,y = C-1/2w とおき, 両辺に左から C1/2 をかけて,アルゴリズム的に解き易い 対称行列の固有値問題
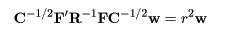
に変換することが多い.